Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
α)
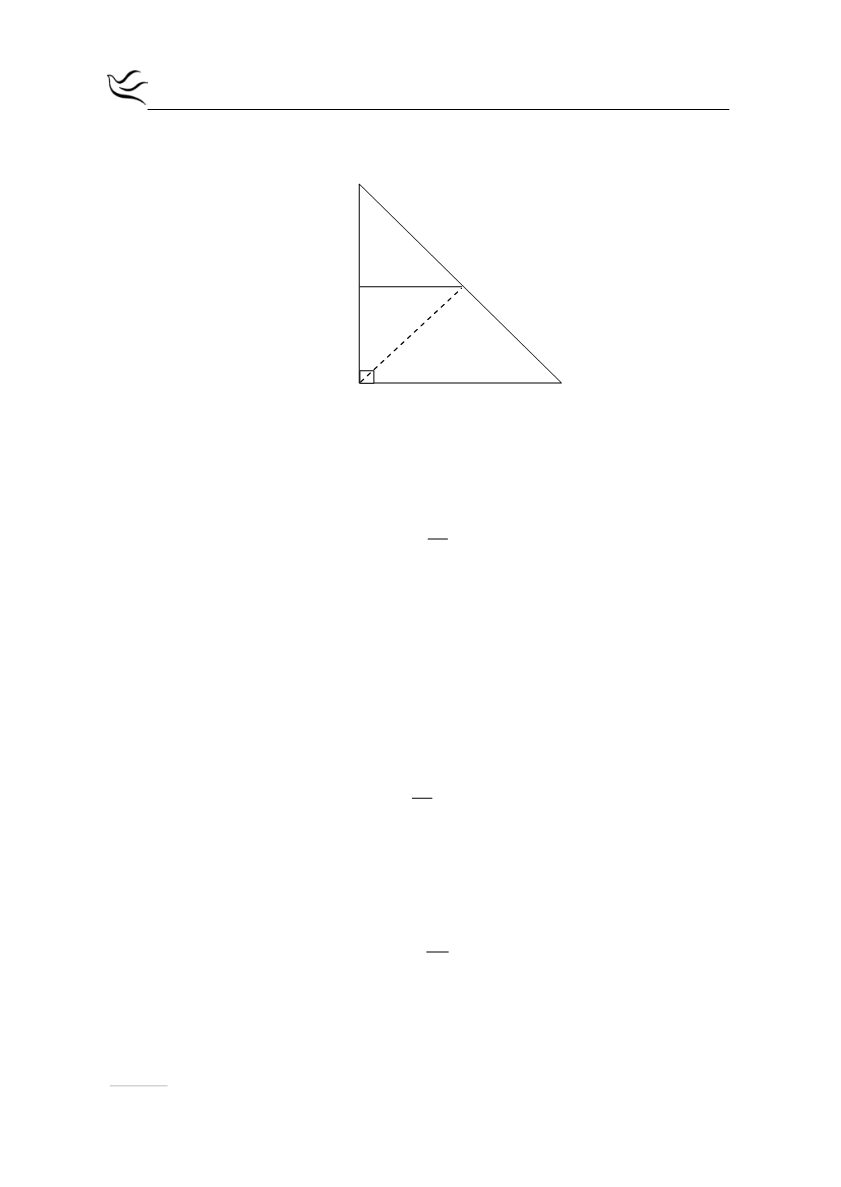
α) Επειδή το τρίγωνο ΑΒΓ είναι ορθογώνιο και ισοσκελές η διχοτόμος ΑΔ της
κορυφής Α θα είναι και διάμεσος που αντιστοιχεί στην υποτείνουσα ΒΓ οπότε
ΒΓ ΑΔ
2
=
.
β) Επειδή
ΑΒ ΑΓ
⊥
και ΔΕ // ΑΒ θα είναι και
ΔΕ ΑΓ
⊥
άρα, το τρίγωνο ΔΕΓ είναι
ορθογώνιο.
γ) Επειδή το τρίγωνο ΑΒΓ είναι ορθογώνιο και ισοσκελές η διχοτόμος ΑΔ της
κορυφής Α θα είναι και ύψος που αντιστοιχεί στην υποτείνουσα ΒΓ οπότε το
τρίγωνο ΑΔΓ θα είναι ορθογώνιο.
Όμως από α) ερώτημα
ΒΓ ΑΔ
ΔΓ
2
= =
δηλαδή το ορθογώνιο τρίγωνο ΑΔΓ είναι και ισοσκελές και επειδή η ΔΕ είναι
ύψος από την κορυφή Δ, που αντιστοιχεί στην υποτείνουσα ΑΓ θα είναι και
διάμεσος άρα,
ΑΓ ΔΕ
2
=
.
Α
Γ
Δ
Ε
Β
48









