Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
β) Σύμφωνα με την εκφώνηση
1
Δ 2Γ
= ⇔
0
60 2Γ
= ⇔
0
Γ 30
=
.
Επίσης,
0
2
0
0
0
1
180
180 60 12
Δ
0
Δ
−
− =
=
=
.
Συνεπώς, στο τρίγωνο ΒΔΓ θα ισχύει
0
2
2
Δ Γ 18
Β
0
+
⇔
+ =
0
0
2
180 12
Β
0 30
= − − ⇔
0
2
Β 30
=
.
Απάντηση:
α) Από τις σχέσεις
Α Γ 2Β
+ =
και
Α 3Γ
=
παίρνουμε
= ⇔
4Γ 2Β
=
2Γ Β
(1).
Σε τρίγωνο ΑΒΓ ισχύουν
Α Γ 2Β
+ =
και
Α 3Γ
=
.
α) Να αποδείξετε ότι η γωνία
Β
είναι 60
0
.
(Μονάδες 10)
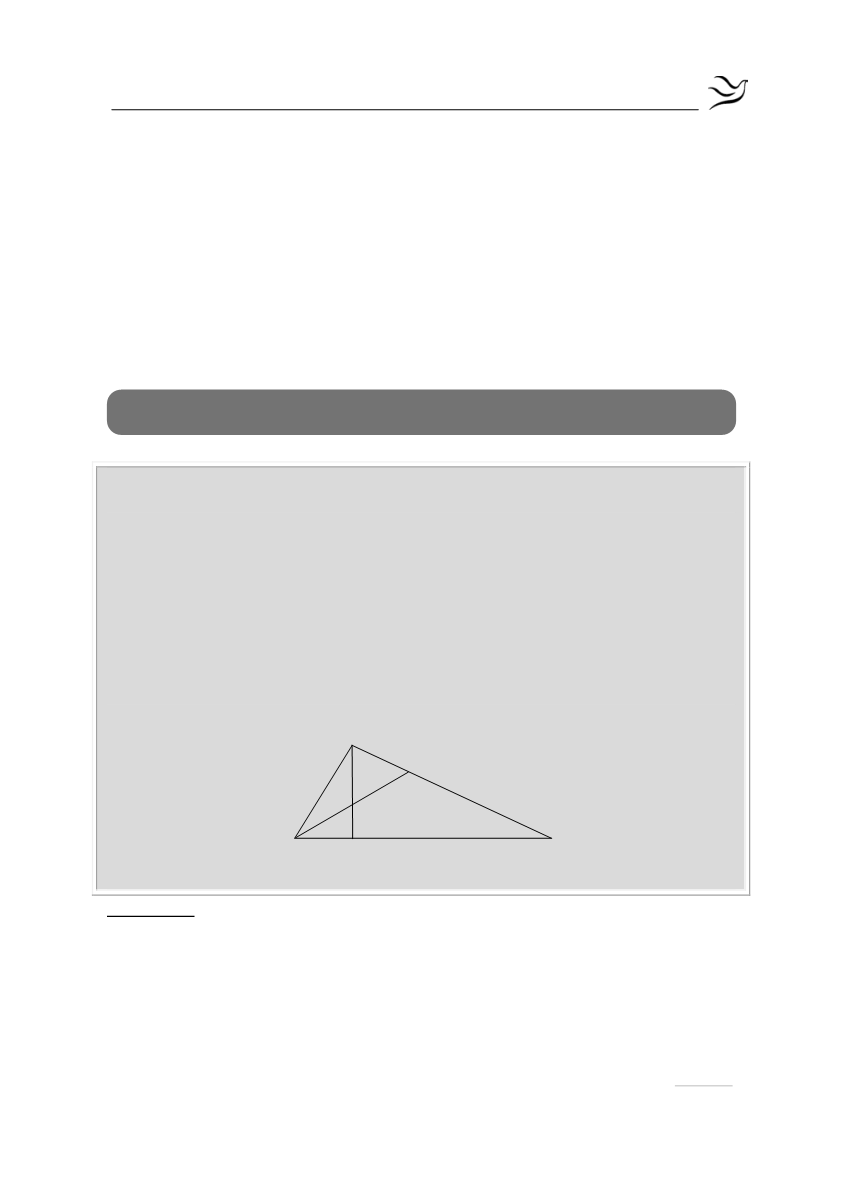
β) Αν το ύψος του ΑΔ και η διχοτόμος του ΒΕ τέμνονται στο σημείο Ζ, να
αποδείξετε ότι το τρίγωνο ΑΖΕ είναι ισόπλευρο.
(Μονάδες 15)
Α
Β
Ε
Δ
Γ
Ζ
ΘΕΜΑ 5578
43









