Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Απάντηση:
Φέρνουμε την ακτίνα ΟΔ του κύκλου.
Το τρίγωνο ΓΔΟ είναι ισοσκελές, αφού ΔΓ=ΔΒ και ΔΒ=ΔΟ ως ακτίνες του
ημικυκλίου άρα,
ΔΓΟ ΔΟΓ x
= =
.
Ομοίως το τρίγωνο ΔΟΕ είναι ισοσκελές, αφού ΟΔ=ΟΕ, ως ακτίνες του
ημικυκλίου άρα,
ΟΔΕ ΟΕΔ y
= =
.
Όμως η γωνία
ΒOΕ
είναι εξωτερική γωνία του τριγώνου ΓΟΕ άρα,
0
x y 45
+ =
(1).
Ακόμη, η γωνία
=
ΟΔΕ y
είναι εξωτερική γωνία του τριγώνου ΔΓΟ, άρα ισχύει
y = 2x (2).
Από τις σχέσεις (1) και (2) έχουμε
0
x 2x 45
+ = ⇔
0
3x 45
= ⇔
0
x 15
=
.
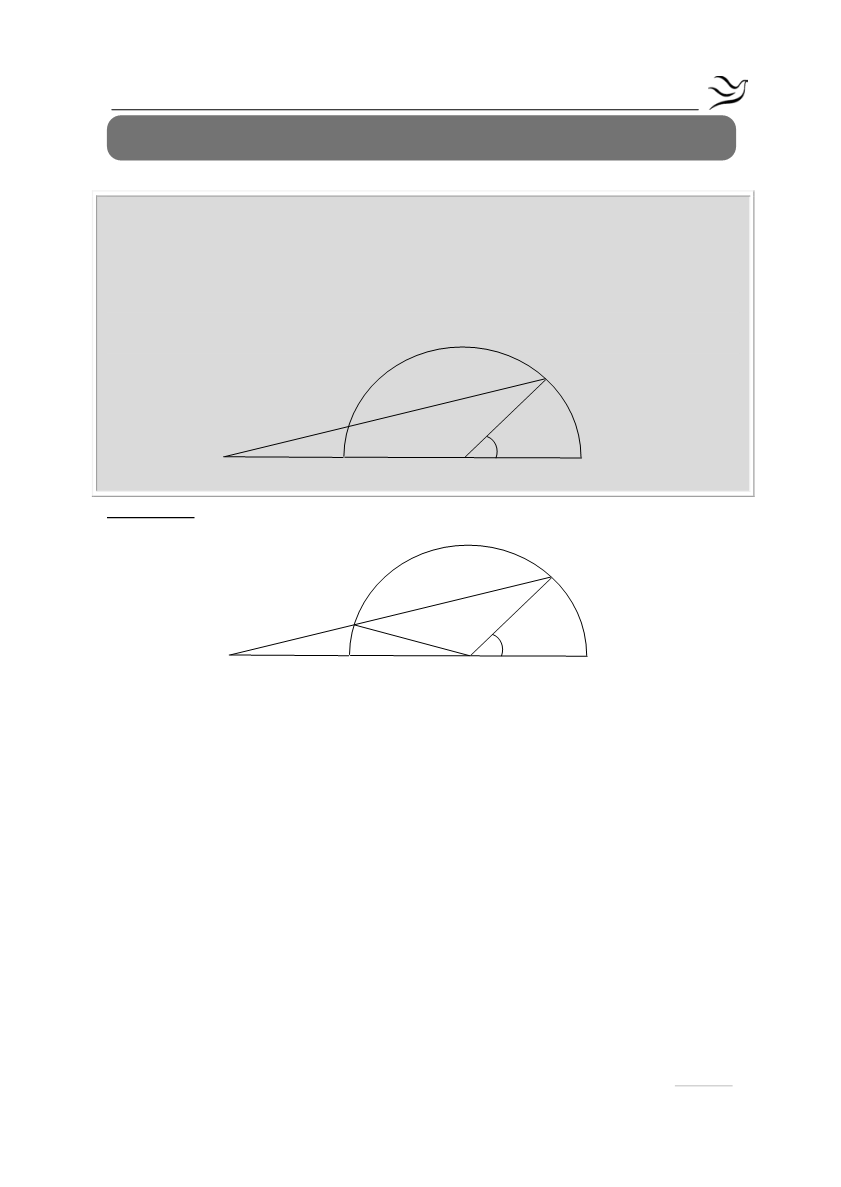
Σε ημικύκλιο διαμέτρου ΑΒ προεκτείνουμε την ΑΒ προς το μέρος του Α και
παίρνουμε ένα σημείο Γ. Θεωρούμε Ε ένα σημείο του ημικυκλίου και έστω Δ το
σημείο τομής του τμήματος ΓΕ με το ημικύκλιο. Αν το τμήμα ΓΔ ισούται με το ΟΒ
και η γωνία
0
ΒΟΕ 45
=
, να υπολογίσετε τη γωνία
ΔΓΟ x
=
.
(Μονάδες 25)
Δ
Γ
Ε
Α
•
Β
Ο
45
0
x
y
y
x
•
•
•
•
•
ΘΕΜΑ 4972
Γ
•
Β
•
•
•
Δ
Ε
Α
Ο
45
0
║
x
•
•
║
39









