Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
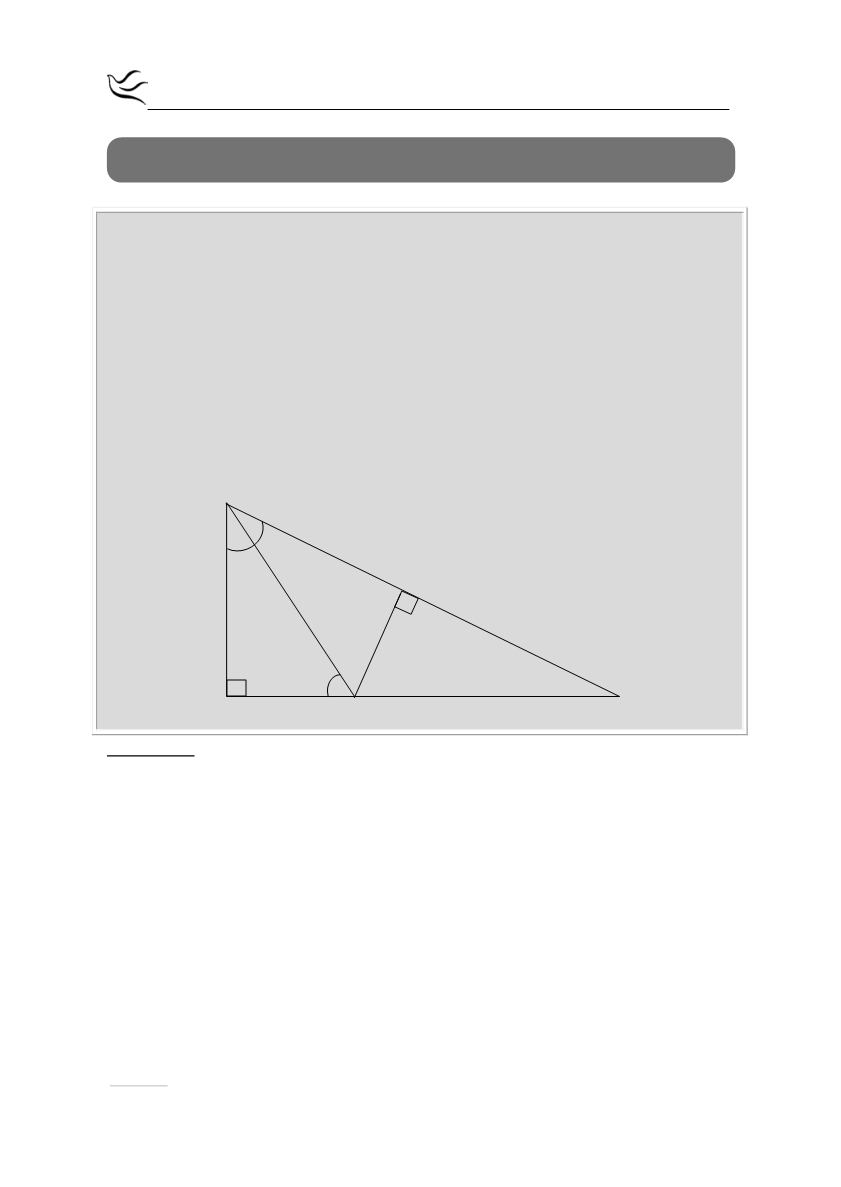
Δίνεται ορθογώνιο τρίγωνο ΑΒΓ (
0
Α 90
=
). Η διχοτόμος της γωνίας
Β
τέμνει την
πλευρά ΑΓ στο σημείο Δ. Φέρουμε τμήμα ΔΕ κάθετο στην πλευρά ΒΓ. Να
αποδείξετε ότι
α) ΒΕ=ΑΒ
(Μονάδες 12)
β) αν επιπλέον
0
ΒΔΑ 55
=
, να υπολογίσετε τις γωνίες του τριγώνου ΓΔΕ.
(Μονάδες 13)
Απάντηση:
α) Το σημείο Δ ανήκει στη διχοτόμο της γωνίας
Β
άρα, ισαπέχει από τις
πλευρές της. Συνεπώς, ΔΑ=ΔΕ (1).
Τα τρίγωνα ΒΑΔ και ΒΕΔ είναι ίσα γιατί
•
0
Α ΒΕΔ 90
= =
•
ΒΔ κοινή και
•
ΔΑ=ΔΕ
άρα, ΒΕ=ΑΒ.
β) Στο ορθογώνιο τρίγωνο ΑΒΔ είναι
Α
Β
Γ
Δ
Ε
55
0
ΘΕΜΑ 2839
32









