Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Απάντηση:
α)
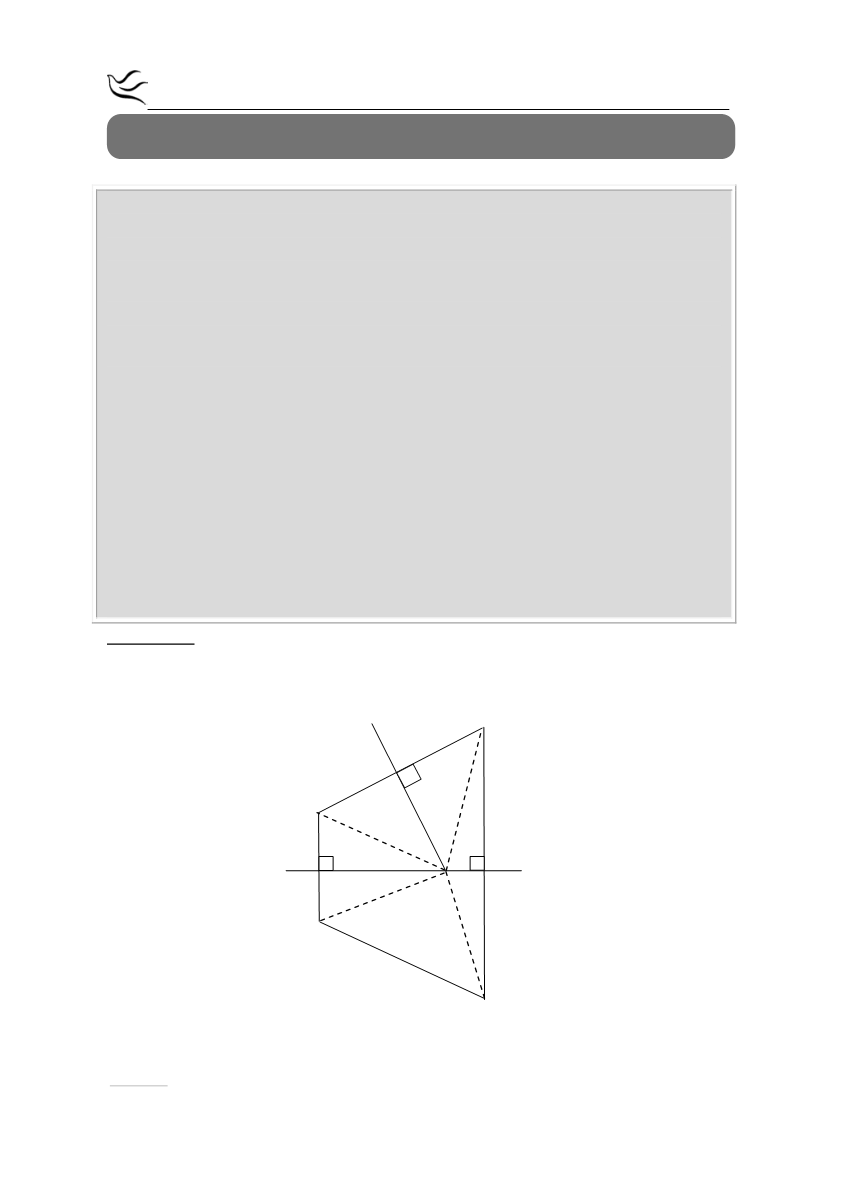
Θεωρούμε ευθεία (ε) και δυο σημεία Α και Β εκτός αυτής, τα οποία
βρίσκονται στο ίδιο ημεπίπεδο σε σχέση με την (ε) έτσι, ώστε η ευθεία ΑΒ να
μην είναι κάθετη στην (ε). Έστω Α' και Β' τα συμμετρικά σημεία των Α και Β
αντίστοιχα ως προς την ευθεία (ε).
α) Αν η μεσοκάθετος του ΑΒ τέμνει την ευθεία (ε) στο σημείο Κ, να
αποδείξετε ότι το Κ ανήκει και στη μεσοκάθετο του Α'Β'.
(Μονάδες 10)
β) Να αποδείξετε ότι το τετράπλευρο ΑΒΒ'Α' είναι τραπέζιο.
(Μονάδες 8)
γ) Να βρείτε τη σχέση των ευθειών ΑΒ και της ευθείας (ε) ώστε το
τετράπλευρο ΑΒΒ'Α' να είναι ορθογώνιο. Να αιτιολογήσετε την απάντησή
σας.
(Μονάδες 7)
Β
Α
Λ
Κ
ε
Μ
Β΄
Α΄
//
//
ΘΕΜΑ 3706
114









