Γεωμετρία A' Λυκείου (Τράπεζα Θεμάτων)

109 / 226

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Απάντηση:
α) Επειδή το ΑΒΓΔ είναι ορθογώνιο παραλληλόγραμμο θα είναι ΟΓ=ΟΔ ως μισά
των ίσων διαγωνίων του ΑΓ και ΒΔ αντίστοιχα. Άρα, το τρίγωνο ΟΔΓ είναι
ισοσκελές με
 = = 0 ΟΔΓ ΟΓΔ 30 (1).
Στο ορθογώνιο τρίγωνο ΔΕΓ με  = 0 ΔΕΓ 90 είναι
 + = ⇔0 ΕΔΓ ΔΓΕ 90  + = ⇔0 0 ΕΔΓ 30 90  = 0 ΕΔΓ 60 (2).
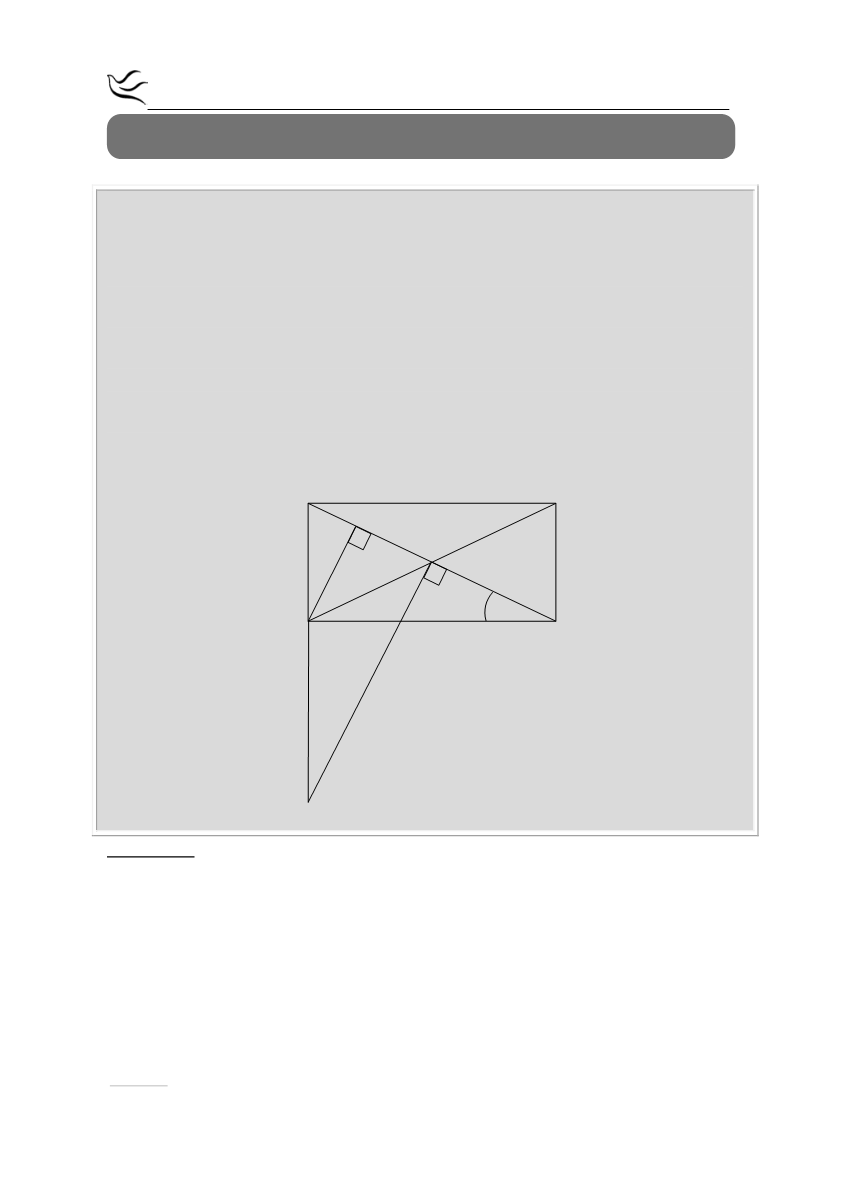
Στο ορθογώνιο παραλληλόγραμμο ΑΒΓΔ είναι  = 0 ΔΓΑ 30 και Ο το κέντρο του.
Φέρουμε ⊥ ΔΕ ΑΓ .
α) Να αποδείξετε ότι η γωνία 
ΑΔΓ χωρίζεται από τη ΔΕ και τη διαγώνιο ΔΒ σε
τρεις ίσες γωνίες.
(Μονάδες 13)
β) Φέρουμε κάθετη στην ΑΓ στο σημείο Ο η οποία τέμνει την προέκταση της ΑΔ
στο Ζ. Να αποδείξετε ότι τα τρίγωνα ΑΖΟ και ΑΒΓ είναι ίσα.
(Μονάδες 12)
Β
Ζ
Γ
A
Δ
Ε
Ο
300
ΘΕΜΑ 3700
108