Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

48 / 146

47
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
(Μονάδες 7)
δ. Να αιτιολογήσετε γραφικά ή αλγεβρικά, γιατί οι συναρτήσεις
    g x f x 3  και     h x f x 3  δεν είναι ούτε άρτιες ούτε περιττές.
(Μονάδες 5)
Απάντηση:
α. Πρέπει:
8 x 0  και 8 x 0  
x 8 και x 8   
8 x 8   
άρα το πεδίο ορισμού είναι:  
f D 8,8 
β. Έχουμε για κάθε f x D ότι και f x D   , επιπλέον:
      f x 8 x 8 x 8 x 8 x           
    8 x 8 x f x        άρα η f είναι περιττή.
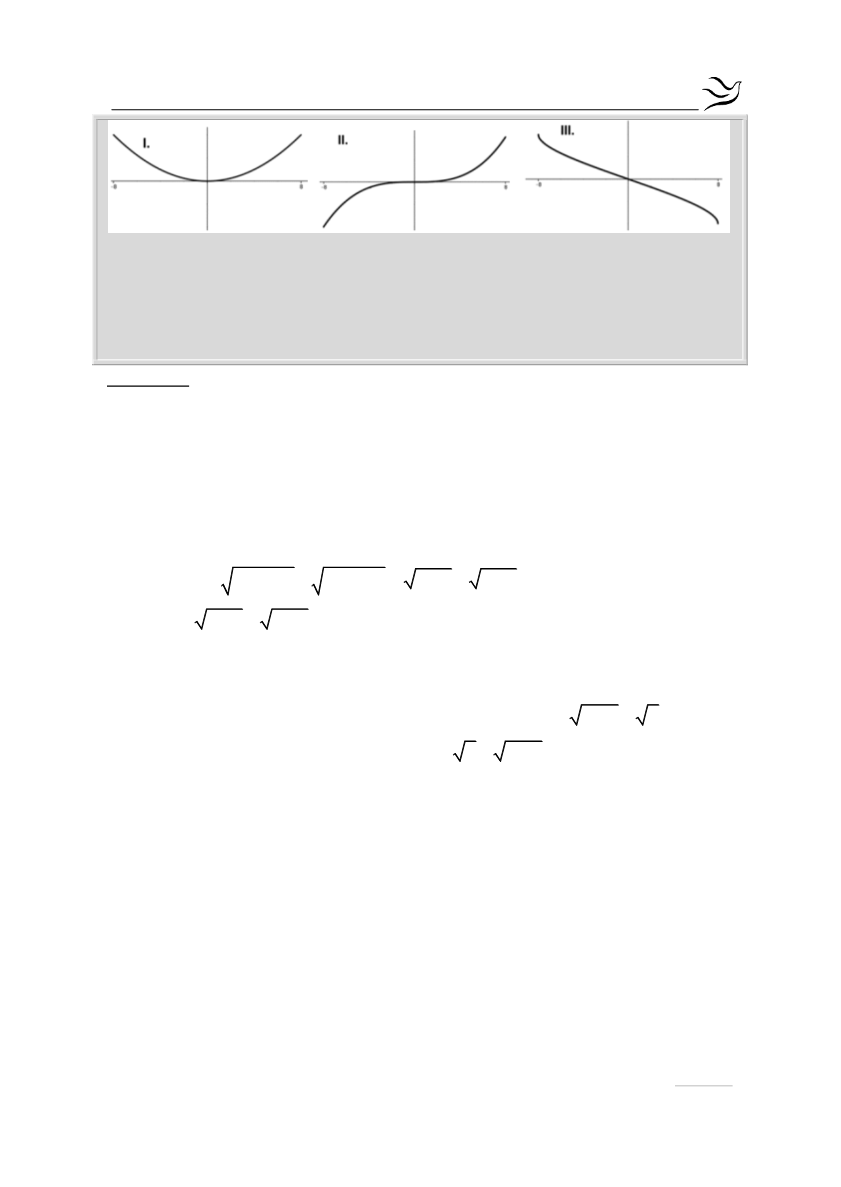
γ. Η μοναδική γνησίως φθίνουσα συνάρτηση είναι η (iii).Από την γραφική
παράσταση λοιπόν παρατηρούμε ότι η f :
παρουσιάζει (ολικό) μέγιστο στο 1 x 8   το   f 8 8 8 0 4      και
(ολικό) ελάχιστο στο 2 x 8 το   f 8 0 8 8 4      .
δ. Η συνάρτηση     g x f x 3   δεν θα είναι ούτε άρτια ούτε περιττή διότι η
γραφική της παράσταση που προκύπτει από την f C μετατοπισμένη κατά
3 μονάδες προς τα κάτω δεν θα είναι συμμετρική ούτε ως προς τον
άξονα y’y ούτε ως προς την αρχή των αξόνων.
Το ίδιο προκύπτει και για την     h x f x 3   της οποίας η γραφική
παράσταση προκύπτει από την f C μετατοπισμένη κατά 3 μονάδες προς
τα αριστερά. Δεν θα είναι συμμετρική ούτε ως προς τον άξονα y’y ούτε
ως προς την αρχή των αξόνων.