Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

21 / 146

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου
20
Συνεπώς για     α,β,γ 1,1,4  το ζεύγος   1,5  θα είναι μοναδική λύση
του συστήματος.
β. Για να είναι το σύστημα αδύνατο θα πρέπει πρώτα D 0 ή πιο απλά, να
έχουμε ίδιους συντελεστές στα α και β, ώστε οι ευθείες να έχουν ίδια
κλίση και ταυτόχρονα οι σταθεροί όροι να είναι διαφορετικοί μεταξύ
τους ώστε οι ευθείες να μην ταυτίζονται.
Άρα για α 2 , β 1 και γ 1   γ 3 το σύστημα θα είναι αδύνατο.
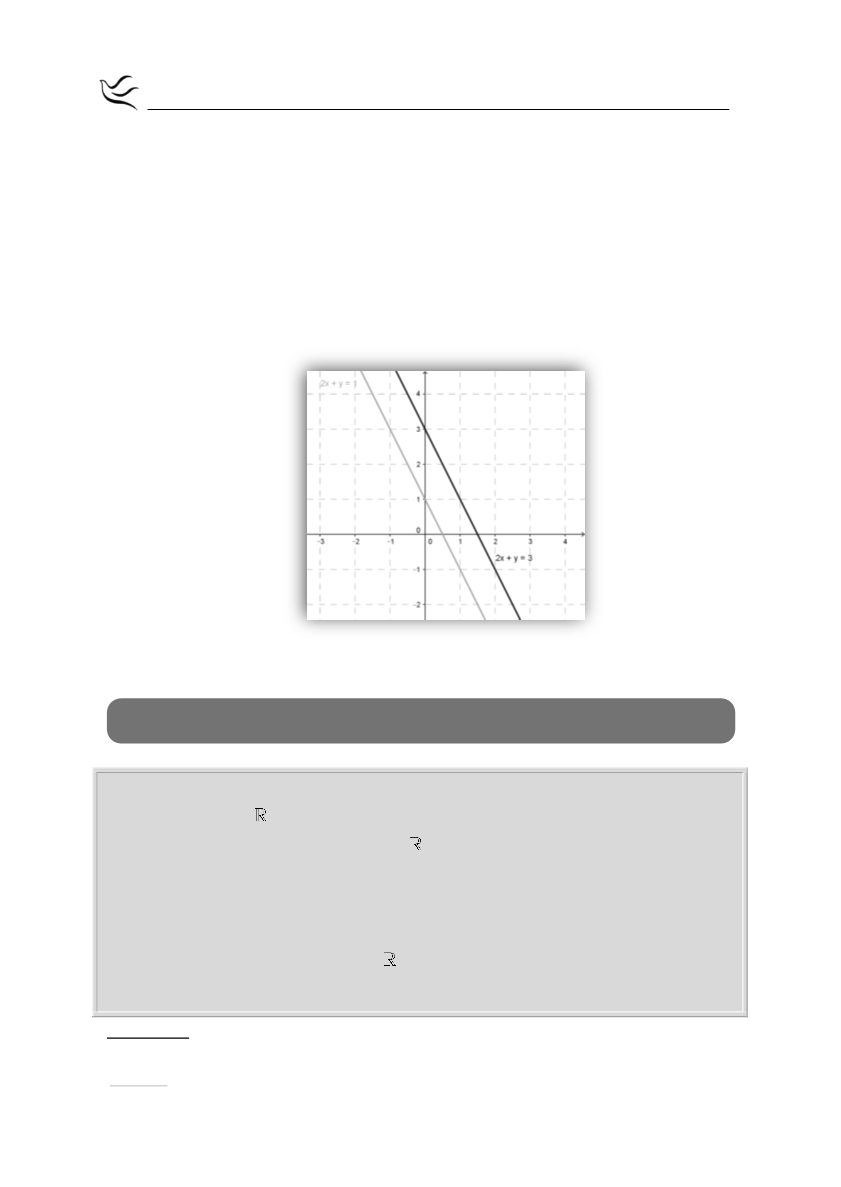
Πράγματι από τις γραφικές τους παραστάσεις διαπιστώνουμε ότι οι δύο
ευθείες δεν έχουν κανένα κοινό σημείο.
Δίνονται οι ευθείες 1 ε και 2 ε με εξισώσεις   x λ 2 y 3   και (λ 2)x 5y 3  
αντίστοιχα και λ  .
α. Για τις διάφορες τιμές του λ  , να βρείτε τη σχετική θέση των δύο
ευθειών. (Μονάδες 13)
β. Στην περίπτωση που οι ευθείες    
1 2 ε , ε τέμνονται, να βρείτε τις
συντεταγμένες του σημείου τομής Α των δύο ευθειών. (Μονάδες 7)
γ. Να βρείτε την τιμή του λ  για την οποία το σημείο Α ανήκει στην
ευθεία με εξίσωση: x 2y 3  . (Μονάδες 5)
Απάντηση:
α. Οι ορίζουσες του συστήματος θα είναι:
ΘΕΜΑ 15. 4-17835