Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

15 / 146

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου
14
Τέλος από την πρώτη εξίσωση για x 1 1 2y 3 2y 4 y 2          ,
άρα το σύστημα έχει μοναδική λύση την     x,y 1,2  .
Δίνονται οι ευθείες με εξισώσεις:    
1 2 ε : 2x y 1 και ε : (λ 1)x y 6       , με
παράμετρο  .
α. Να βρείτε την τιμή του  ώστε οι ευθείες  
1  και  2  να είναι
παράλληλες. (Μονάδες 8)
β. Να παραστήσετε γραφικά τις  
1  και  
2  , για 3   . (Μονάδες 8)
γ. Υπάρχει τιμή του   , ώστε οι ευθείες  
1  και  
2  να ταυτίζονται;
Να δικαιολογήσετε την απάντησή σας. (Μονάδες 9)
Απάντηση :
α. Για να είναι οι ευθείες παράλληλες θα πρέπει να έχουν ίδιο συντελεστή
διεύθυνσης.
 1 1 ε : 2x y 1 y 2x 1 λ 2
       
     
2 2 ε : x y 6 y= x 6 λ λ 1 λ 1 λ 1
        
Έχουμε λοιπόν: 1 2 1 2 1 2 3          
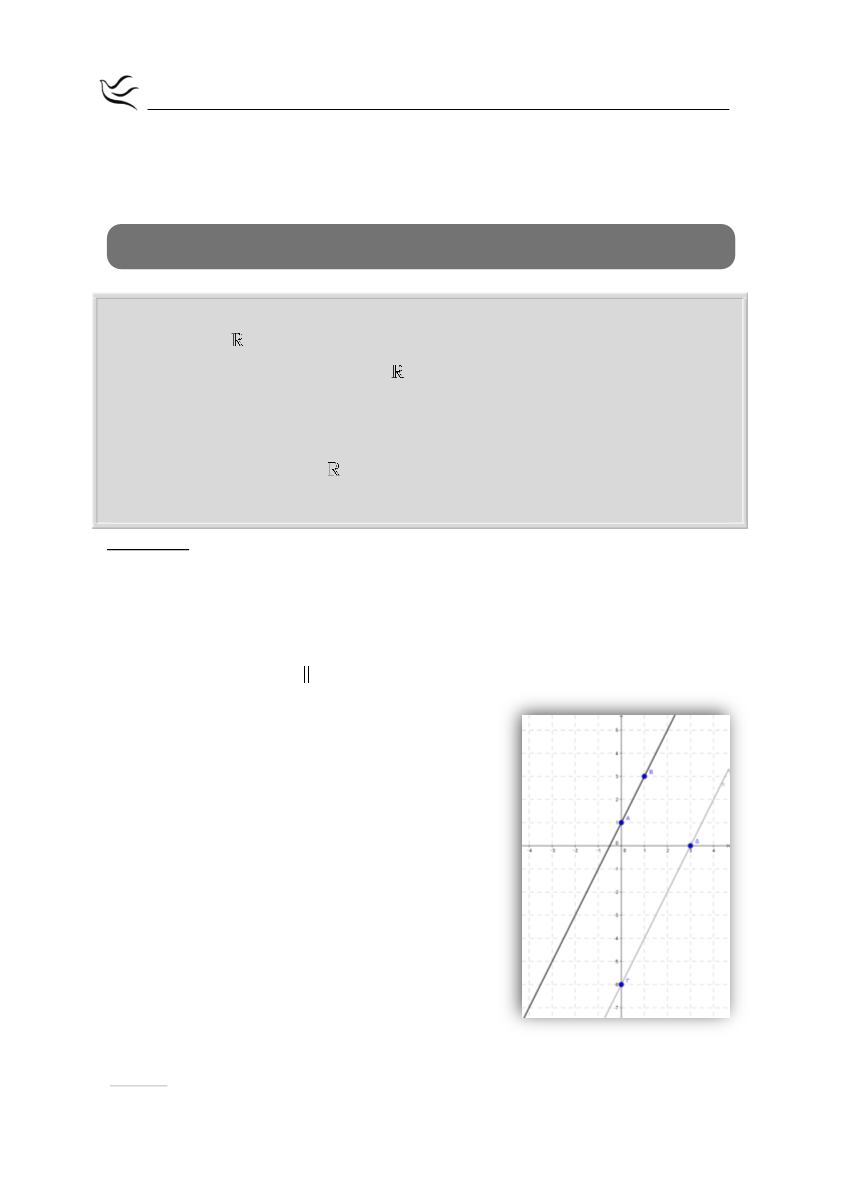
β. Για 3   :
 1 : y 2x 1    και  
2 : y 2x 6   
Για να σχεδιάσουμε τις ευθείες
βρίσκουμε 2 σημεία για την καθεμία
 1 ε : για x 0 y 1    και για
x 1 y 3   άρα η ευθεία θα
διέρχεται από τα   A 0,1 και   B 1,3 .
 2 ε : για x 0 y 6     και για
y 0 x 3   άρα η ευθεία θα
διέρχεται από τα   Γ 0, 6 και   Δ 3,0
.
γ. Για να ταυτίζονται οι δύο ευθείες, θα
πρέπει οι εξισώσεις τους να είναι ίδιες,
δηλαδή, όλοι οι αντίστοιχοι συντελεστές
ΘΕΜΑ 9. 2-17703