133
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Απάντηση
:
α.
Το πολυώνυμο έχει παράγοντα το
x 1
, που σημαίνει ότι:
3
2
P 1 0
1 α 1 β 1 6 0
α β 5 0 β α 5
1
.
Επίσης ξέρουμε ότι: η αριθμητική τιμή του για
x 2
είναι ίση με 12
άρα:
P 2 12
3
2
2
α 2 β 2 6 12
4α 2β 14 12
2α β 1 0
2
Από τη
2
μέσω της
1
έχουμε:
2α α 5 1 0
3α 6
α 2
από
1
για
α
2
β
2 5 β 3
.
β.
i. Για
α 2
και
β 3
το πολυώνυμο γίνεται:
3
2
P x x 2x 3x 6
Από το σχήμα Horner για
ρ 2
έχουμε:
1
-2
3
6
2
2
0
6
1
0
3
12
Άρα:
2
P x x
3 x 2
12
.
ii. Έχουμε:
P x x 14
2
x 3 x 2 12 x 14
2
x
3 x 2 12 x 14 0
2
x 3 x 2 x 2 0
2
x 2 x
3 1 0
2
x 2 x 2
0
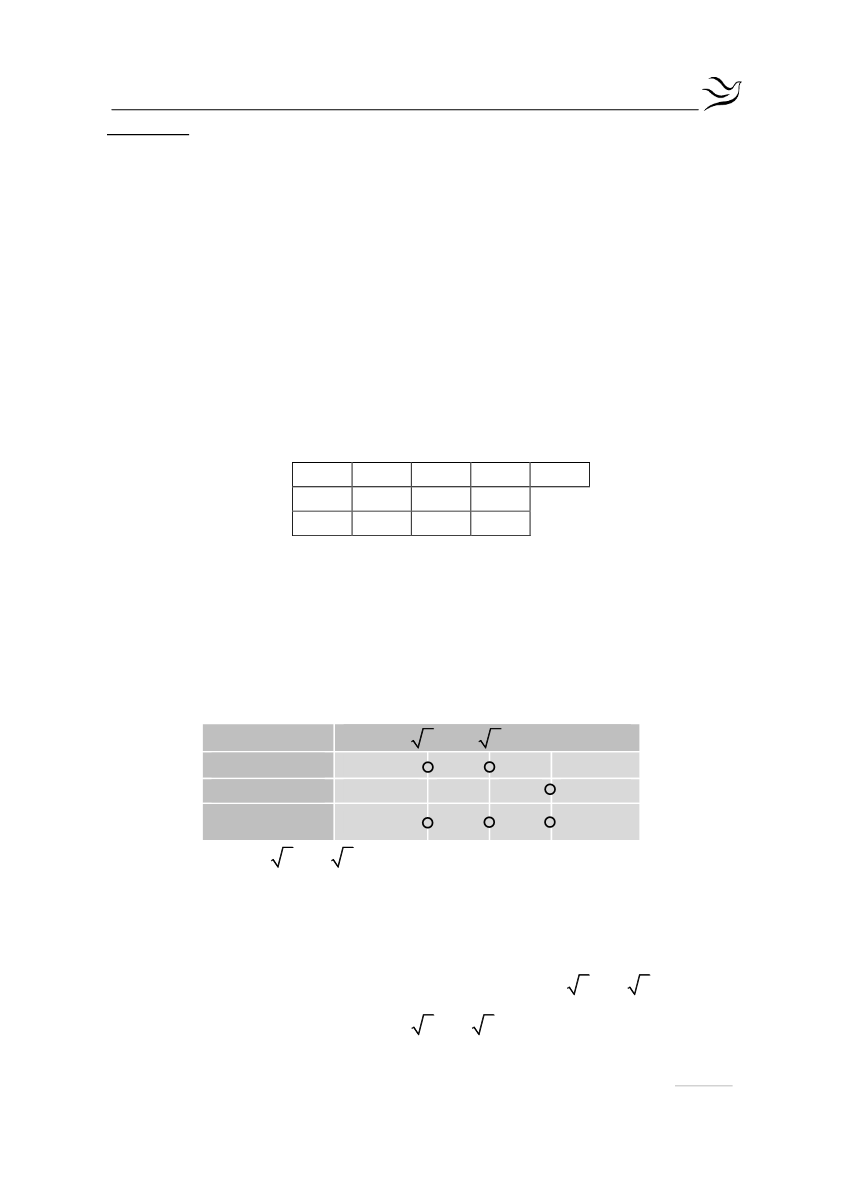
από τον πίνακα προσήμων έχουμε ότι:
2 2 2 +
2
x
2
+
-
+
+
x 2
-
-
-
+
2
x 2 x 2
-
+
-
+
Άρα
x
,
2
2,2
.
iii. Έχουμε
P lnx lnx 14
για
x
0
.
θέτουμε
lnx
t
συνεπώς η ανίσωση γίνεται:
P t
t 14
από το προηγούμενο ερώτημα έχουμε ότι
t
,
2
2,2
άρα
lnx
,
2
2,2









