Αλγεβρα A' Λυκείου (Τράπεζα Θεμάτων)

95 / 240

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου
94
2 4 16 12 4 0        
και ρίζες τους αριθμούς
1,2
4 2
x ,
6

 δηλαδή 1 2
1
x x 1.
3
  
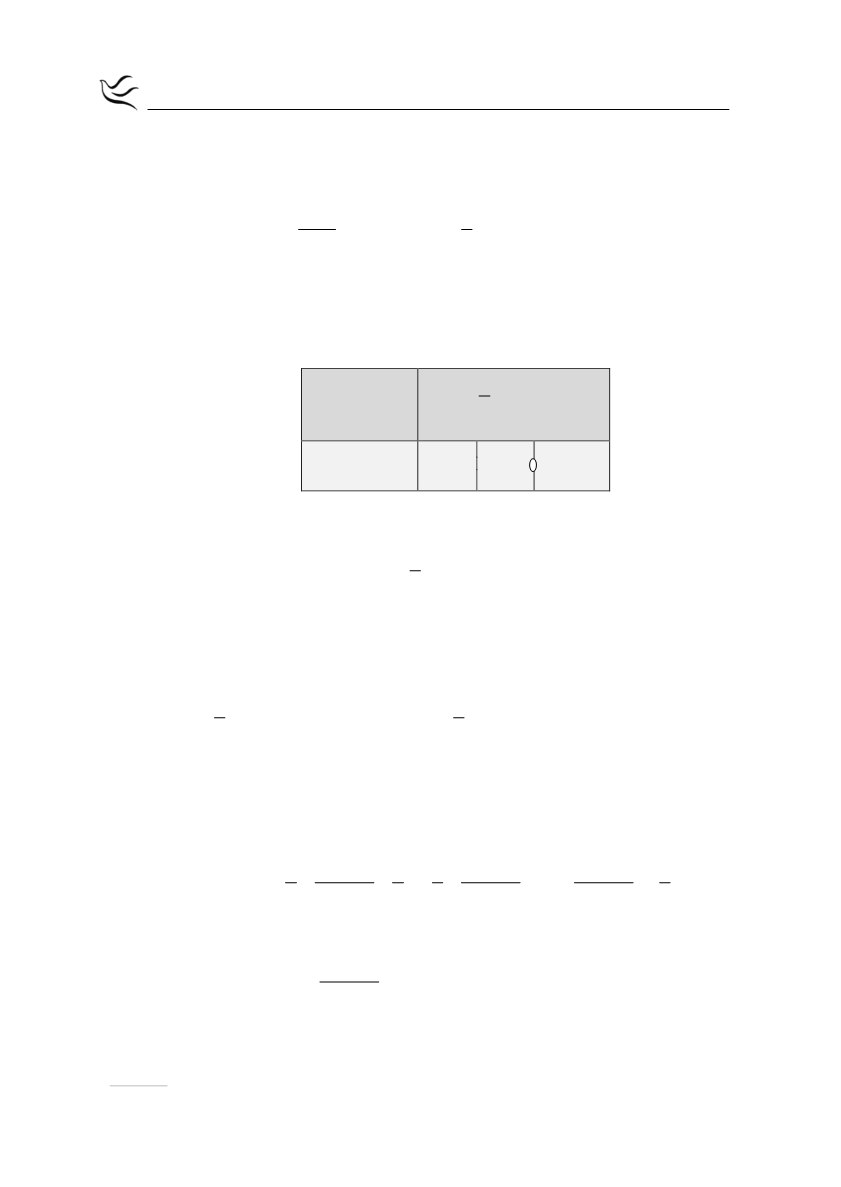
Οι ρίζες και το πρόσημο του τριωνύμου 2 3x 4x 1   φαίνονται στον
παρακάτω πίνακα
Επομένως, 2 1
3x 4x 1 0 x , 1 .
3
 
      
 
β) Εφόσον οι αριθμοί α, β είναι λύσεις της παραπάνω ανίσωσης, έχουμε
1
1 1 3 3
3
       και
1
1 2 6 6
3
      .
Από τις σχέσεις αυτές, προσθέτοντας κατά μέλη, παίρνουμε
3 3 6 9 1 3 6 3 6 1
3 3 6 9 1 , 1 .
9 9 9 3 9 9 3
          
              
 
Επομένως, ο αριθμός
3 6
9
 
είναι λύση της δοθείσας ανίσωσης.
x 
1
3
1 
2
3x 4x 1    