87
Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Για την ανίσωση
(2)
έχουμε
2
2
x
16 0
x 16
x
4 4 x 4
β)
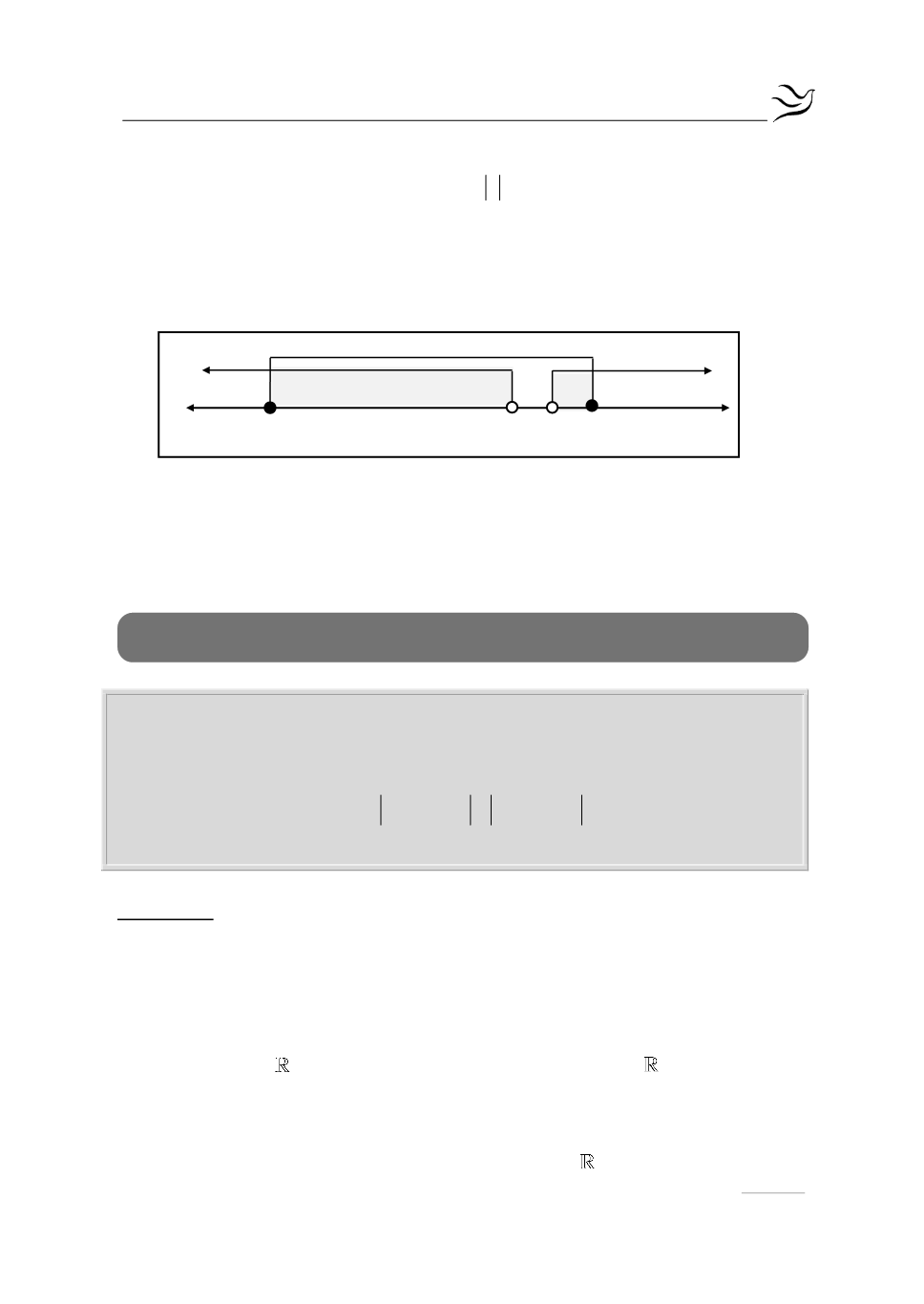
Οι λύσεις κάθε εξίσωσης φαίνονται στον παρακάτω άξονα των πραγματικών
αριθμών :
Τελικά, οι κοινές λύσεις των παραπάνω ανισώσεων είναι οι αριθμοί
x 4,2 (3,4]
.
α)
Να αποδείξετε ότι
2
x 4x 5 0
, για κάθε πραγματικό αριθμό x.
(Μονάδες 10)
β)
Να γράψετε χωρίς απόλυτες τιμές την παράσταση
2
2
B
x
4x 5 x 4x 4
(Μονάδες 15)
Απάντηση:
α)
Το τριώνυμο
2
x 4x 5
έχει διακρίνουσα
2
4 4 5
4 0
και συνεπώς διατηρεί το πρόσημο του συντελεστή του
2
x ,
που είναι θετικό
για κάθε
x
.
Δηλαδή,
2
x
4x 5 0
ά x
.
β)
Αποδείξαμε ότι:
2
x 4x 5 0
για κάθε
x
ΘΕΜΑ 2-1544
–5 –4 –3 –2 –1 0 1 2 3 4 5 6









