75
Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
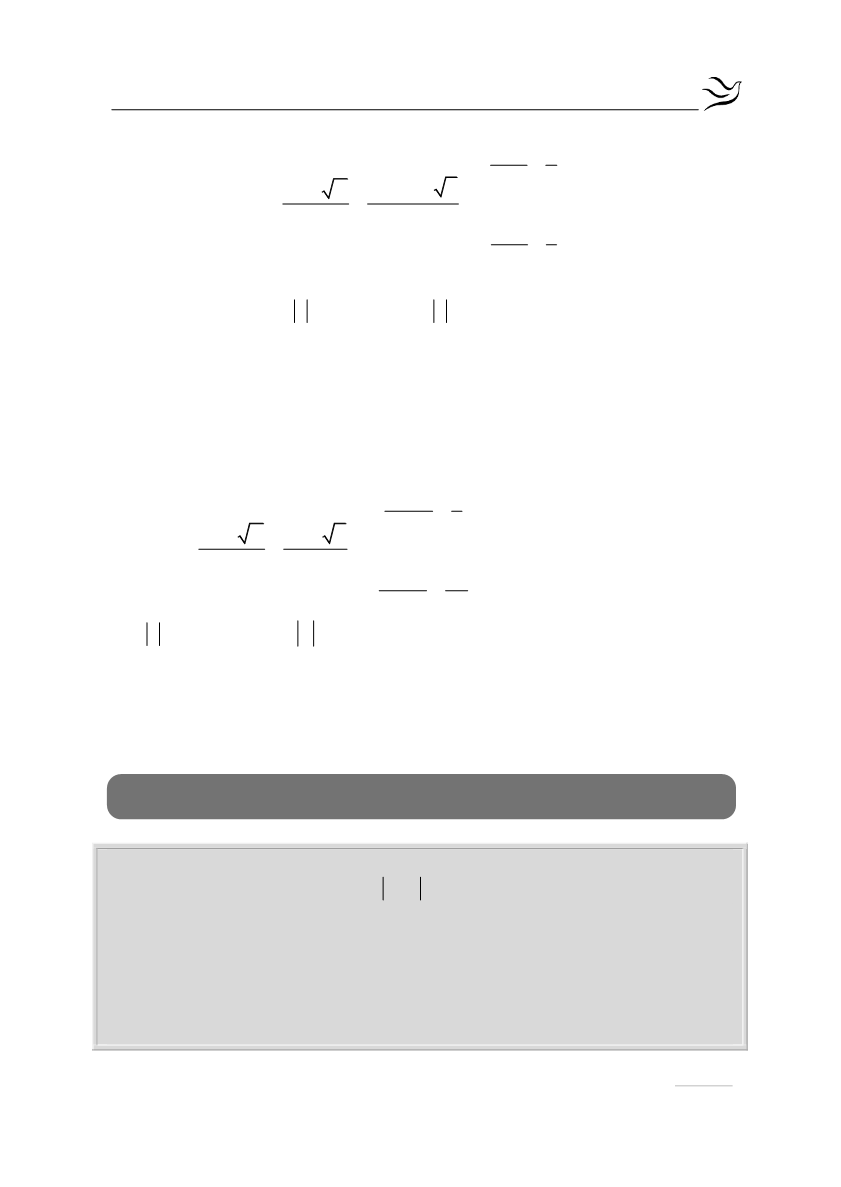
1,2
4 4
1
2
2
=
4 2 6
3
2 2
ή
4 2 2
1
2 2
άρα
ω 1 ή ω 3
, οπότε
x 1
x 1
ή
x
3 x
3
Όμοια για
4
έχουμε
2
4
3 0
,
όπου
α 1, β 4 και γ 3
και διακρίνουσα
2
2
4 4
4 1 3 4
με ρίζες
1,2
2
4 4
2 1
=
4 2 2
1
2 2
ή
4 2 6
3
2 2
άρα
ω
1 ή ω 3
Άρα
x 1
αδύνατη ή
αδύνατη.
Επομένως για
η εξίσωση
δεν έχει πραγματικές ρίζες.
Δίνεται η ανίσωση
x 1 4
(1)
α) Να λύσετε την ανίσωση και να παραστήσετε το σύνολο των λύσεων
της πάνω στον άξονα των πραγματικών αριθμών.
( Μονάδες 7)
β) Να βρείτε όλες τις ακέραιες λύσεις της ανίσωσης (1).
(Μονάδες 3)
x 3
β
4
1
ΘΕΜΑ 4-7677









