Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου
64
1 2
w w
0
1
.
Δηλαδή οι ρίζες
1
2
w ,w
είναι ετερόσημες. Έστω ότι
1
w
0
και
2
w
0
(απορρίπτεται).
Επομένως, η εξίσωση
(1)
ισοδύναμα γράφεται
2
2
1
2
x
w ή x
w ,
αδύνατον.
Δηλαδή,
2
1
1
x
w x w
.
Τελικά, η εξίσωση
(1)
έχει δυο μόνο διαφορετικές πραγματικές ρίζες.
Τα σπίτια τεσσάρων μαθητών, της Άννας, του Βαγγέλη, του Γιώργου και
της
Δήμητρας βρίσκονται πάνω σε ένα ευθύγραμμο δρόμο, ο οποίος ξεκινάει
από
το σχολείο τους. Οι αποστάσεις των τεσσάρων αυτών σπιτιών από το
σχολείο,
A B
S ,S ,S ,S
, αντίστοιχα ικανοποιούν τις σχέσεις
A
B
S S
,
S 3S
S
4
και
S
S S
S
.
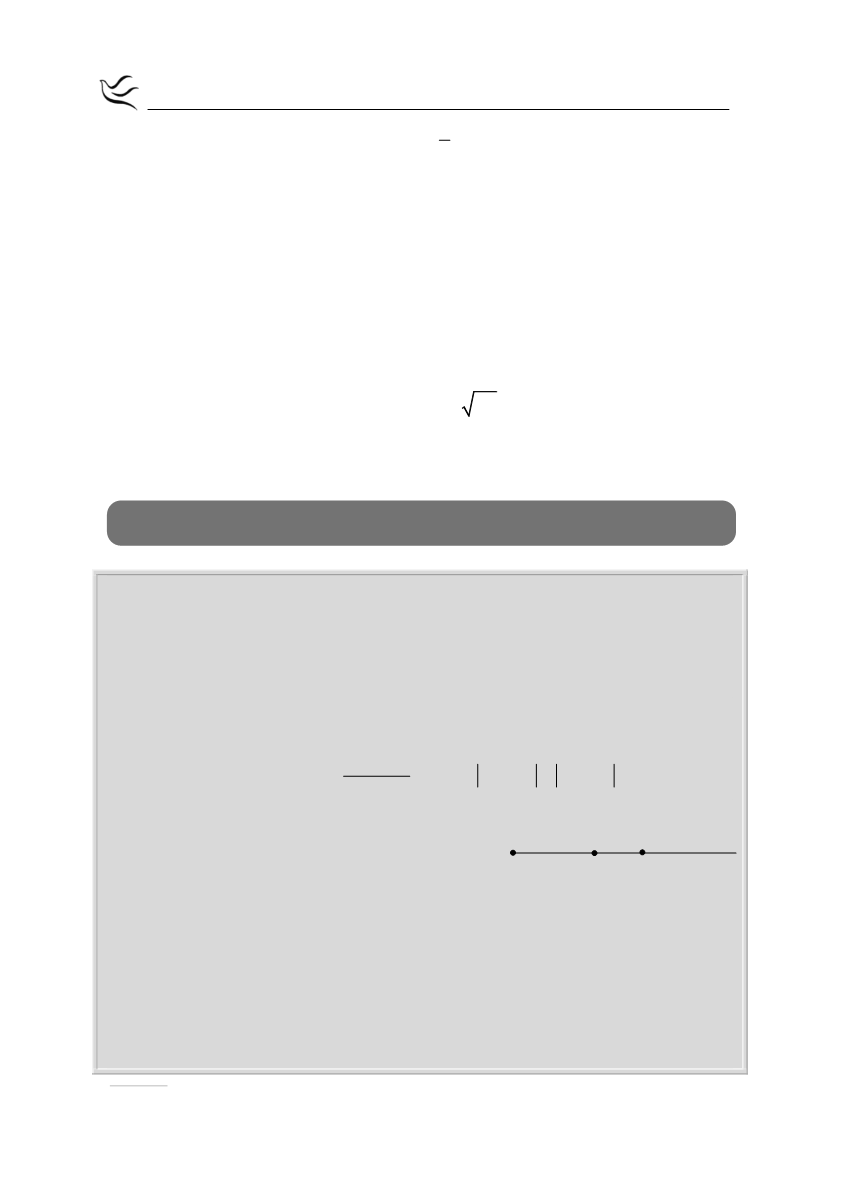
Στον διπλανό άξονα, το σχολείο
βρίσκεται στο σημείο Ο και τα σημεία
Α, Β παριστάνουν τις θέσεις των
σπιτιών της Άννας και του Βαγγέλη
αντίστοιχα.
α) Να τοποθετήσετε πάνω στον άξονα τα σημεία Γ και Δ που
παριστάνουν τις θέσεις των σπιτιών του Γιώργου και της Δήμητρας.
Να αιτιολογήσετε την απάντηση σας.
(Μονάδες 12)
β) Αν επιπλέον, οι τιμές των αποστάσεων
A
B
S , S
σε Km ικανοποιούν
τις σχέσεις
A B
S S
1,4
και
A B
S
S
0,45
, τότε:
ΘΕΜΑ 4-7510
Α
O
B









