Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου
24
Απάντηση:
α)
Η παράσταση
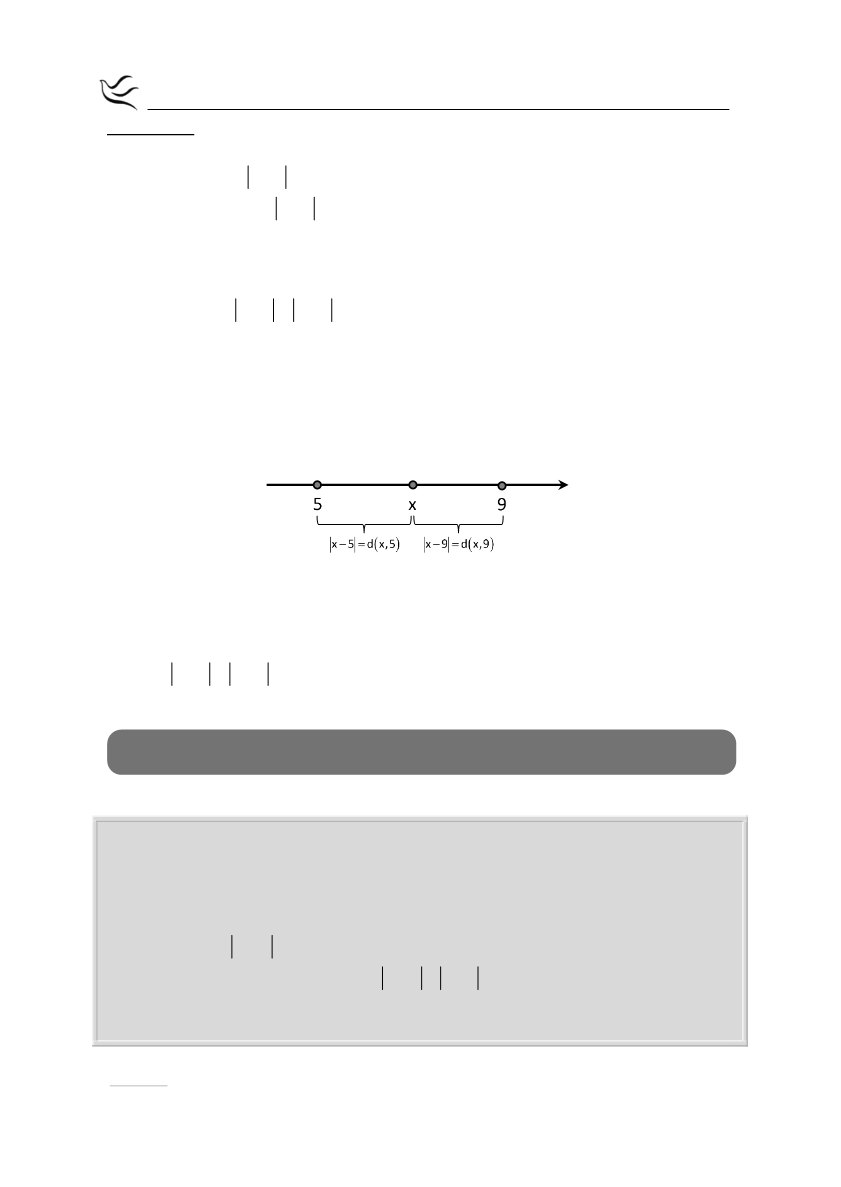
x 5 d x,5
συμβολίζει την απόσταση του σημείου Μ από
το Α. Η παράσταση
x 9 d x,9
συμβολίζει την απόσταση του σημείου Μ
από το Β.
β)
i)
Έχουμε,
x 5
x 9
d x,5 d x,9 MA
MB
Τα Α, Β, Μ είναι συνευθειακά και το Μ ισαπέχει από τα Α, Β άρα το Μ είναι
μέσον του ευθύγραμμου τμήματος ΑΒ.
ii)
Τα σημεία Α, Β και Μ παριστάνονται στον παρακάτω άξονα:
Εφόσον το σημείο Μ είναι το μέσον του τμήματος ΑΒ, θα παριστάνει τον
αριθμό 7. Αλγεβρικά μπορούμε να το αποδείξουμε χρησιμοποιώντας τη σχέση:
x 5 x 9
5 9, αδύνατη
x 5 x 9
ή
ή
x 7
x 5 x 9
2x 14
.
Δίνονται οι πραγματικοί αριθμοί
α
και
β
για τους οποίους ισχύει η ανισότητα:
α 1 1 β
0
.
α)
Να αποδείξετε ότι το
1
είναι μεταξύ των
α , β
.
(Μονάδες 13)
β)
Αν επιπλέον
β α 4
, να υπολογίσετε την τιμή της παράστασης:
Κ α 1
1 β
.
Να αιτιολογήσετε την απάντησή σας είτε γεωμετρικά είτε αλγεβρικά.
(Μονάδες 12)
Α
Μ
Β
ΘΕΜΑ 4-7791









