Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου
20
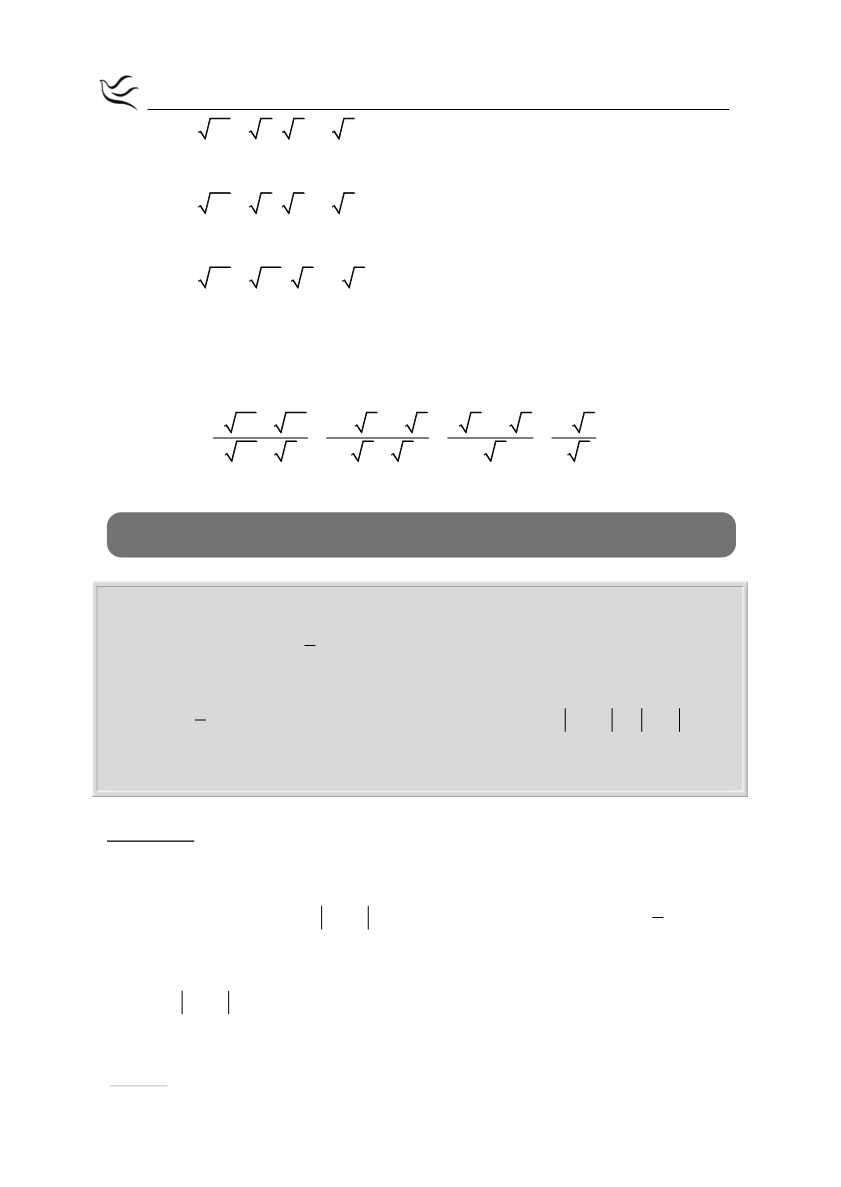
20 4 5 2 5 2 2,24 4,48
.
45 9 5 3 5 3 2,24 6,72
.
80 16 5 4 5 4 2,24 8,96
.
β)
Σύμφωνα με το α) ερώτημα θα είναι:
3 20 80
3 2 5 4 5 6 5 4 5 10 5
5
45 5 3 5
5
2 5
2 5
.
Για τον πραγματικό αριθμό
x
ισχύει:
d 2x,3 3 2x
.
α)
Να αποδείξετε ότι
3
x
2
.
(Μονάδες 12)
β)
Αν
3
x
2
, να αποδείξετε ότι η παράσταση:
K 2x 3 2 3 x
είναι
ανεξάρτητη του
x
.
(Μονάδες 13)
Απάντηση:
α)
Έχουμε διαδοχικά:
3
d 2x,3 3 2x 2x 3 3 2x 2x 3 0 2x 3 x
2
.
β)
Είναι:
2x 3 3 2x
, σύμφωνα με την εκφώνηση. Επιπλέον:
ΘΕΜΑ 2–3884









