Αλγεβρα A' Λυκείου (Τράπεζα Θεμάτων)

218 / 240

217
Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
 Αν   x 2 x 2 0, τότε x 2 x 2        , οπότε   f x x 3  
Δηλαδή,  
 
 
x 3, x 2 α
f x
x 3, x 2 β
  

 
  

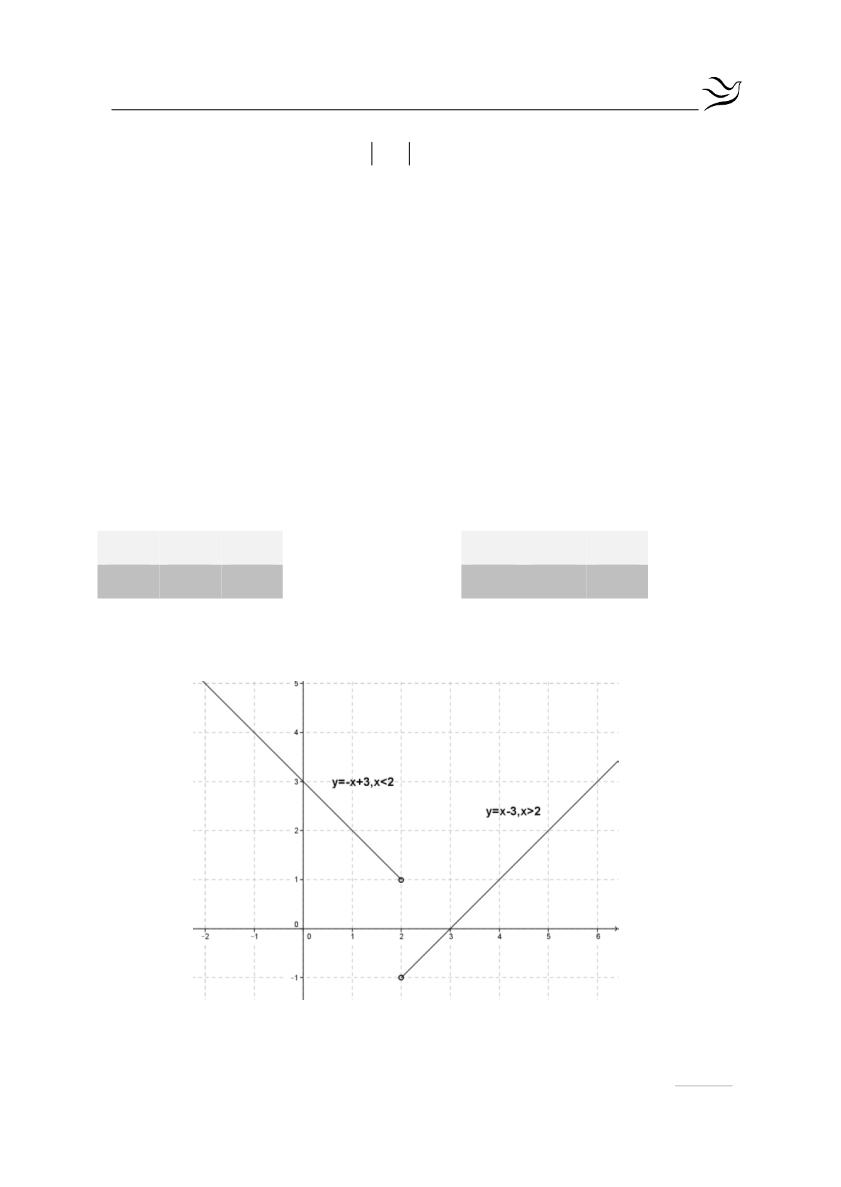
γ) H γραφική παράσταση της συνάρτηση f αποτελείται από τις δύο ημι-
ευθείες y x 3, x 2   και y x 3, x 2    από τις οποίες έχει εξαιρεθεί η
αρχή τους.
Έχουμε
y x 3, x 2   y x 3, x 2   
x 3 4 x 0 –1
y 0 1 y 3 4