Αλγεβρα A' Λυκείου (Τράπεζα Θεμάτων)

145 / 240

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου
144
ii) Τα μήκη α, β είναι οι ρίζες της εξίσωσης 2 x 10x 1 0    , η οποία έχει
διακρίνουσα
 2
10 4 96 0       .
Επομένως,
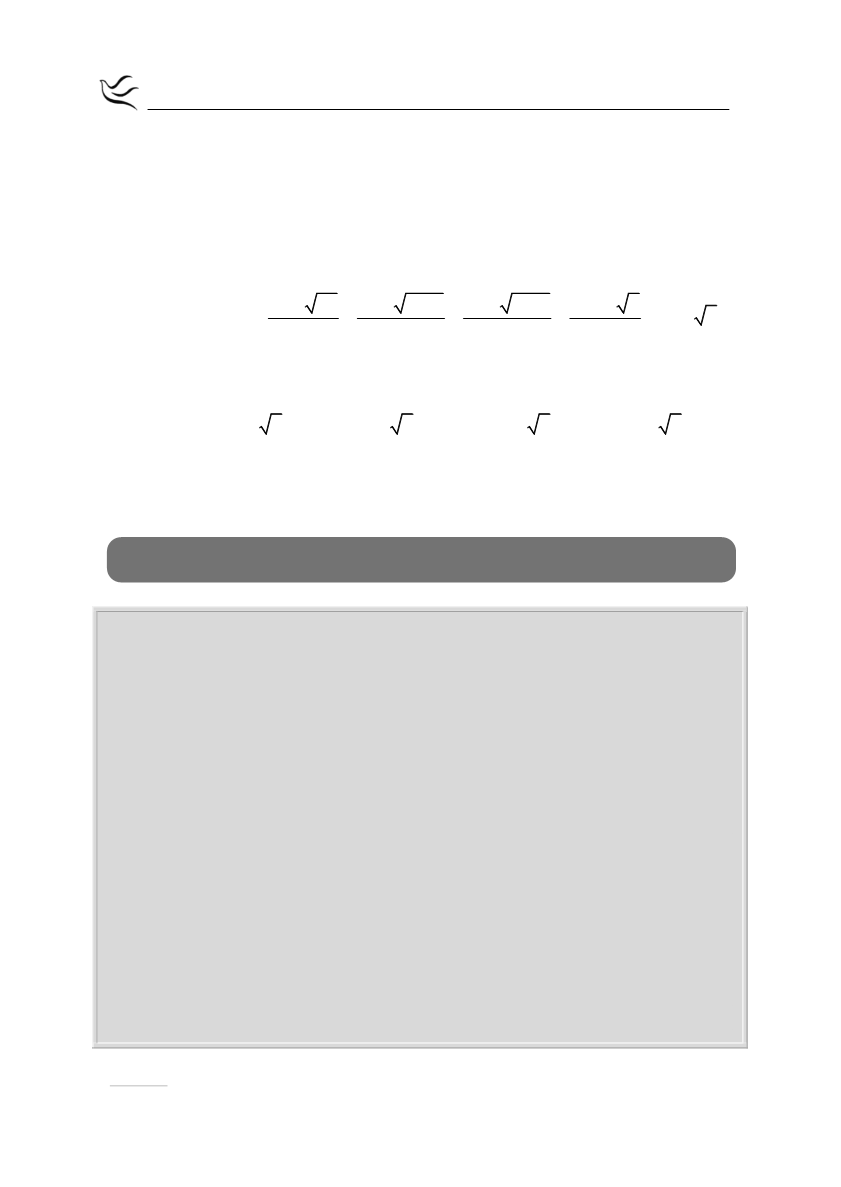
10 96 10 8 12 10 16 6 10 4 6
, 5 2 6
2 2 2 2
     
       
Δηλαδή,
 
5 2 6 5 2 6        ή  
5 2 6 5 2 6        .
Δίνονται οι αριθμοί 2 , x , 8 με x 0 .
α. Να βρείτε την τιμή του x ώστε οι αριθμοί 2 , x , 8 , με τη σειρά που δίνονται,
να αποτελούν διαδοχικούς όρους αριθμητικής προόδου. Ποια είναι η
διαφορά ω αυτής της προόδου;
(Μονάδες 5)
β. Να βρείτε τώρα την τιμή του x ώστε οι αριθμοί 2 , x , 8 , με τη σειρά που
δίνονται, να αποτελούν διαδοχικούς όρους γεωμετρικής προόδου. Ποιος είναι
ο λόγος λ αυτής της προόδου;
(Μονάδες 5)
γ) Αν    είναι η αριθμητική πρόοδος 2,5,8 ,11, ... και    είναι η
γεωμετρική πρόοδος 2 , 4 , 8 , 16 , ... τότε:
*i. Να βρείτε το άθροισμα S  των  πρώτων όρων της  
  .
(Μονάδες 7)
*ii. Να βρείτε την τιμή του  ώστε, για το άθροισμα S των  πρώτων όρων
της    να ισχύει:   7 2 S 24
   .
(Μονάδες 8)
ΘΕΜΑ 4-6859