Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

128 / 130

127
Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’ – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
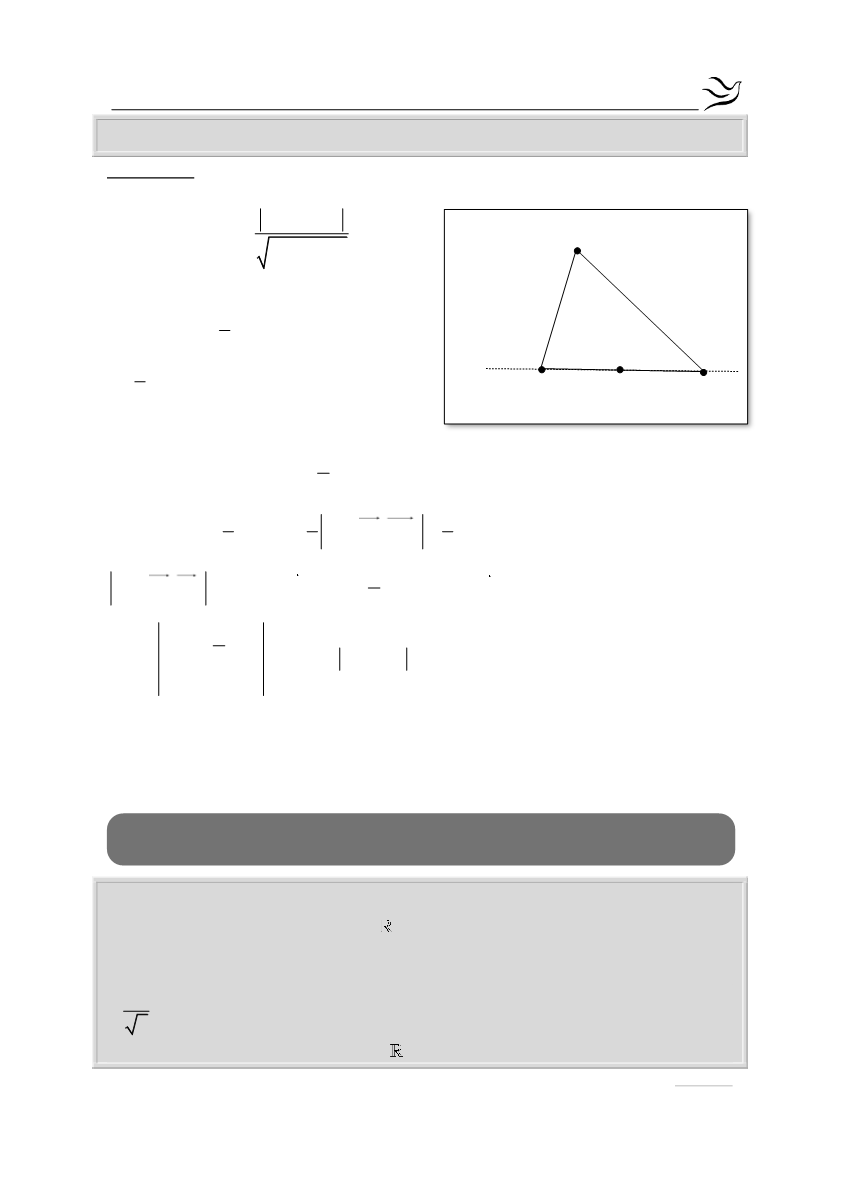
γ. Να βρείτε τις συντεταγμένες των κορυφών Β και Γ.
Απάντηση:
α. Είναι  
 2
2
12 18 9
d A,BΓ 3
4 3
 
 
 
β. Είναι
 
     
1
ΑΒΓ 45 βυ 45
2
1
ΒΓ d Α,ΒΓ 45 ΒΓ 30
2
   
   
γ. Έστω   Β x,y όμως το Β ανήκει στην
ε: 4x 3y 9 0   άρα
4
B x, x 3
3
 
 
 
είναι       1 1 1
ABM ABΓ det AB,AM 45
2 2 2
   
 
det AB,AΓ 45 με
4
ΑΒ x 3, x 9
3
 
   
 
και   AM 0, 5 
Έτσι:
4
x 3 x 9
| | 45 5x 15 45 3
0 5
 
     

5x 15 45    ή 5x 15 45     
x 6  ή x 12
Άρα   B 6, 11  και   Γ 12,13 ή   Β 12,13 και   Γ 6, 11  .
Δίνεται η εξίσωση     (ε): λ 2 x 2λ 1 y 2 λ 0       .
α. Δείξτε ότι για κάθε τιμή του λ  η παραπάνω εξίσωση παριστάνει ευθείες
που περνάνε από το ίδιο σημείο, το οποίο να βρείτε.
β. Βρείτε για ποια τιμή του λ, η απόσταση του Α(2,2) από τη ευθεία (ε) είναι
3
5
.
γ. Να βρείτε για ποιες τιμές του λ  η ευθεία (ε) είναι :
ΘΕΜΑ 8
Γ Β
Α(3,6)
M(3,1)
4x-3y-9=0