Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

126 / 130

125
Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’ – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Έτσι 2 δ / /θ με
2 δ
2β β
λ
8 4
  

και θ λ 1  και
2 θ δ
β
λ λ 1 β 4
4
     
Άρα το   Κ 4,4
δ. Η ακτίνα του κύκλου θα είναι   ρ d 0,Κ 
    2 2
ρ 4 0 4 0 ρ 16 16 32       
άρα ο ζητούμενος κύκλος έχει εξίσωση 2 2
x y 32   .
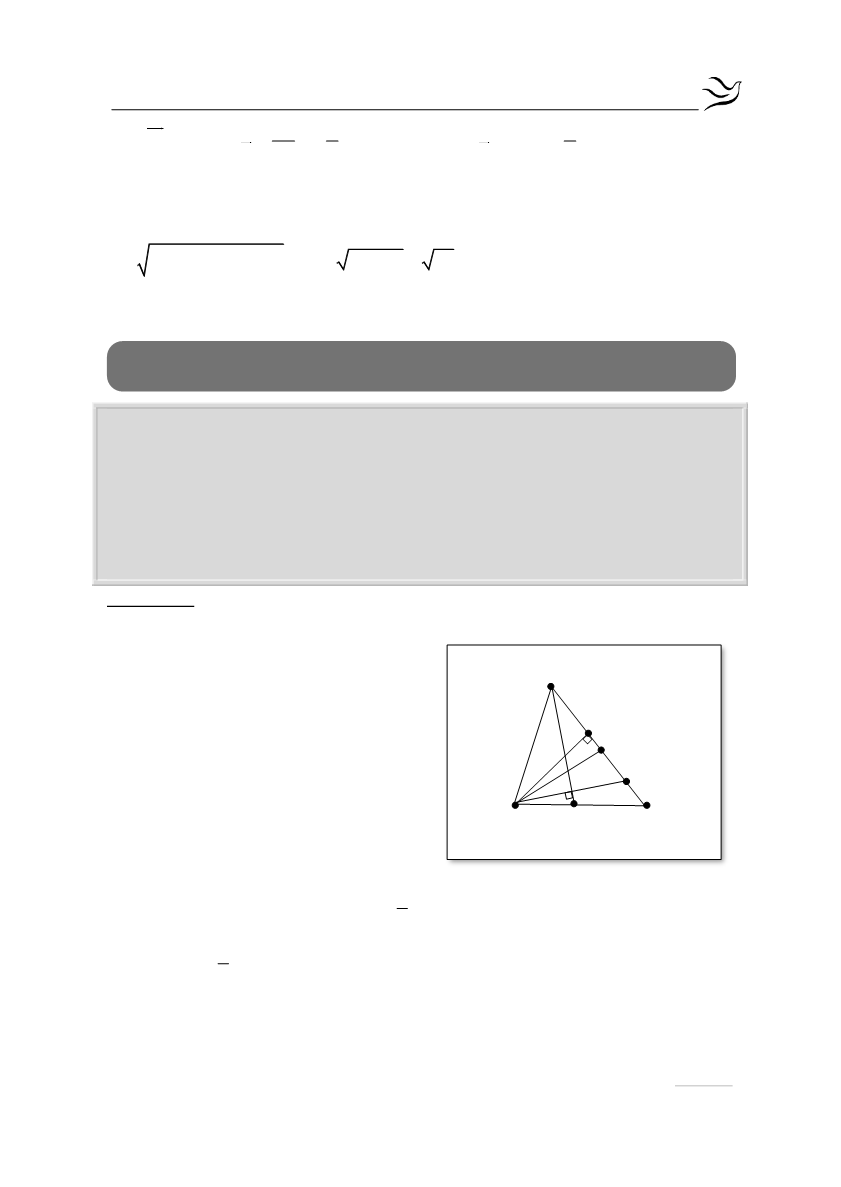
Δίνεται τρίγωνο ΑΒΓ του οποίου γνωρίζουμε την εξίσωση της διχοτόμου
ΑΔ : 3x y 10  , την εξίσωση του ύψους BE: x y 6  , την εξίσωση της
διαμέσου ΒΣ:13x 3y 8  . Να βρείτε:
α. τις συντεταγμένες της κορυφής Β.
β. το συμμετρικό του Β ως προς την ΑΔ έστω Μ.
γ. την εξίσωση της ΑΓ.
δ. τις συντεταγμένες των κορυφών Α και Γ.
Απάντηση:
α. Το σημείο Β είναι σημείο τομής των ΒΕ και ΒΣ
Έτσι:
x y 6 3x 3y 18
13x 3y 8 13x 3y 8
      
 
   
 
x 1
10x 10
y 7
  
   
  
Άρα   B 1, 7  .
β. Θα βρούμε την ευθεία ε που είναι
κάθετη στην ΑΔ και διέρχεται από το Β
Είναι ΑΔ ε ε ε
1
λ λ 1 3λ 1 λ
3
       .
Έτσι   1
ε: y 7 x 1 x 3y 20 0
3
       .
Θα βρούμε το ίχνος έστω Κ, που είναι το σημείο τομής των δύο ευθειών ε και
ΑΔ, έτσι με σύστημα έχουμε :
ΘΕΜΑ 6
Γ
Β
Α
Ε
Σ
Δ
M
K