Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

123 / 130

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’
122
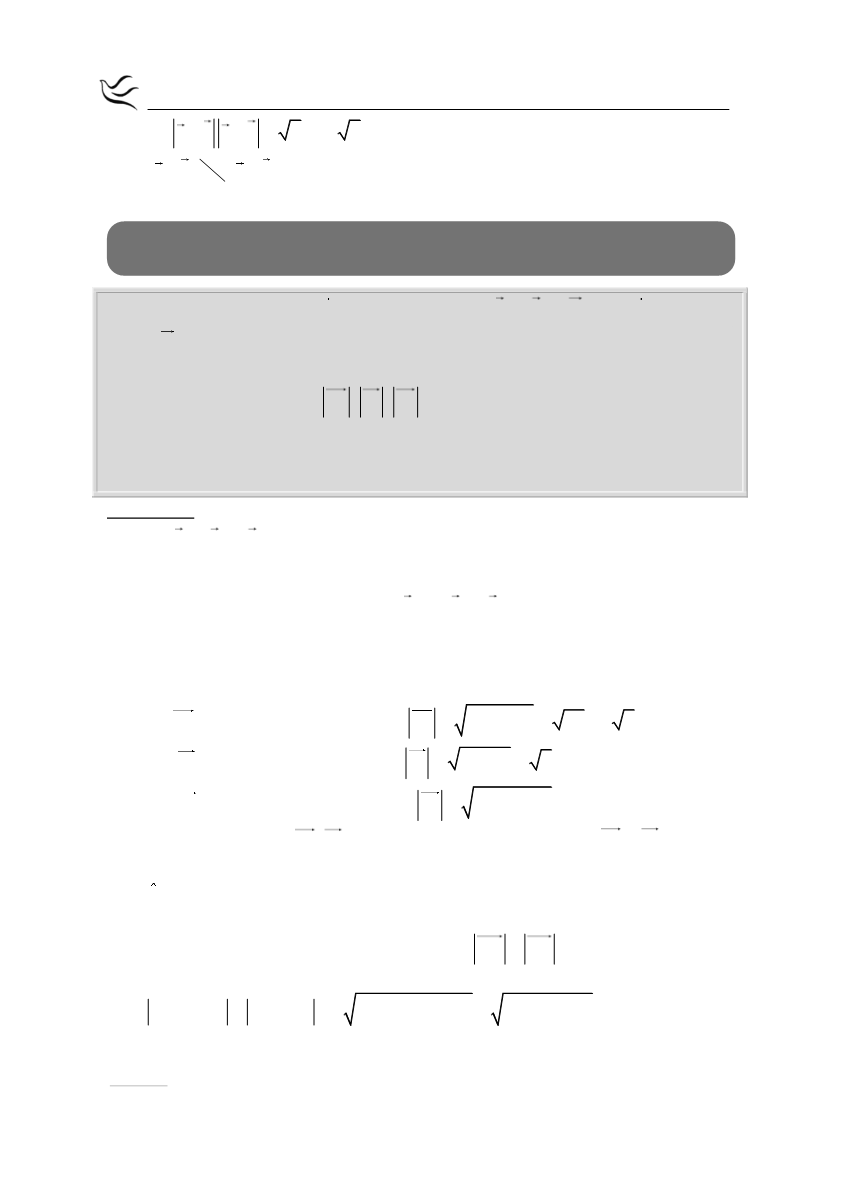
 α β α β 62 2 6   
Άρα  
α β / /  
α β .
Α. Να γραφεί το διάνυσμα   u 2,6  στη μορφή u λv μw  όπου   v 2, 1 
και   w 3,1 και λ,μ πραγματικοί αριθμοί.
Β. Δίνονται τα σημεία Α(5,-1), Β(1,1), Γ(2,3).
α. Να βρεθούν τα μήκη ΑΒ , ΒΓ , ΑΓ .
β. Να μελετηθεί το είδος του τριγώνου ΑΒΓ.
γ. Να βρεθεί σημείο Μ στον άξονα xx', ώστε το τρίγωνο ΜΑΒ να είναι
ισοσκελές με κορυφή το Μ.
Απάντηση:
A. Είναι       u λv μw 2,6 λ 2, 1 μ 3,1           2,6 2λ 3μ, λ μ       
2 2λ 3μ λ 4
6 λ μ μ 2
     
 
    
άρα, u 4v 2w   
B. α. Διαδοχικά έχουμε:
     ΑΒ 1 5,1 1 4,2      με  2 2
ΑΒ 4 2 20 2 5    
     ΒΓ 2 1,3 1 1,2    με 2 2
ΒΓ 1 2 5   
     ΑΓ 2 5,3 1 3,4      με  2 2 ΑΓ 3 4 5    
β. Παρατηρούμε ότι    ΑΒ ΒΓ 4,2 1,2 4 4 0        , άρα, ΑΒ ΒΓ δηλαδή
ο Β 90 άρα το ΑΒΓ είναι ορθογώνιο τρίγωνο
γ. Έστω   Μ x,0 αφού είναι στον x’x πρέπει MA MB 
          2 2 2 2
5 x, 1 1 x,1 5 x 1 1 x 1            x 4   .
Άρα,   M 4,0 .
ΘΕΜΑ 3