Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
28
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
x
x'(x 1) x(x 1)' x 1 2x x 1 x 1
'
f '(x)
0
x 1
(x 1)
(x 1)
(x 1)
(x 1)
- - -
- - - -
+
æ
ö
=
=
=
=
= -
<
ç
÷-
-
-
-
-
è
ø
για κάθε
{ }
x
1,1
Î - -
.
Γ.
Είναι:
2
x 1
x 1
x 1
x 1
x
x(x 1)
x 1
lim[(x 1) f(x)] lim (x 1)
lim
lim
x 1
(x 1)(x 1)
x 1 2
®-
®-
®-
®-
+ é
ù
é
ù
+ ×
=
+ ×
=
=
=
ê
ú
ê
ú-
+ -
-
ë
û
ë
û
.
Δ.
Αν ω είναι η γωνία που σχηματίζει η εφαπτόμενη της γραφικής παράστασης
της
f
στο σημείο
( )
(
)
0, f 0
με τον άξονα
x
΄
x
, τότε θα έχουμε
:
( )
εφω f ' 0
=
.
Όμως,
2
2
2
0 1
f
΄(0)
1
(0 1)
+
= -
= -
-
και επειδή
ο
0
ω 180
£ <
,
προκύπτει
ο
ω 135
=
.
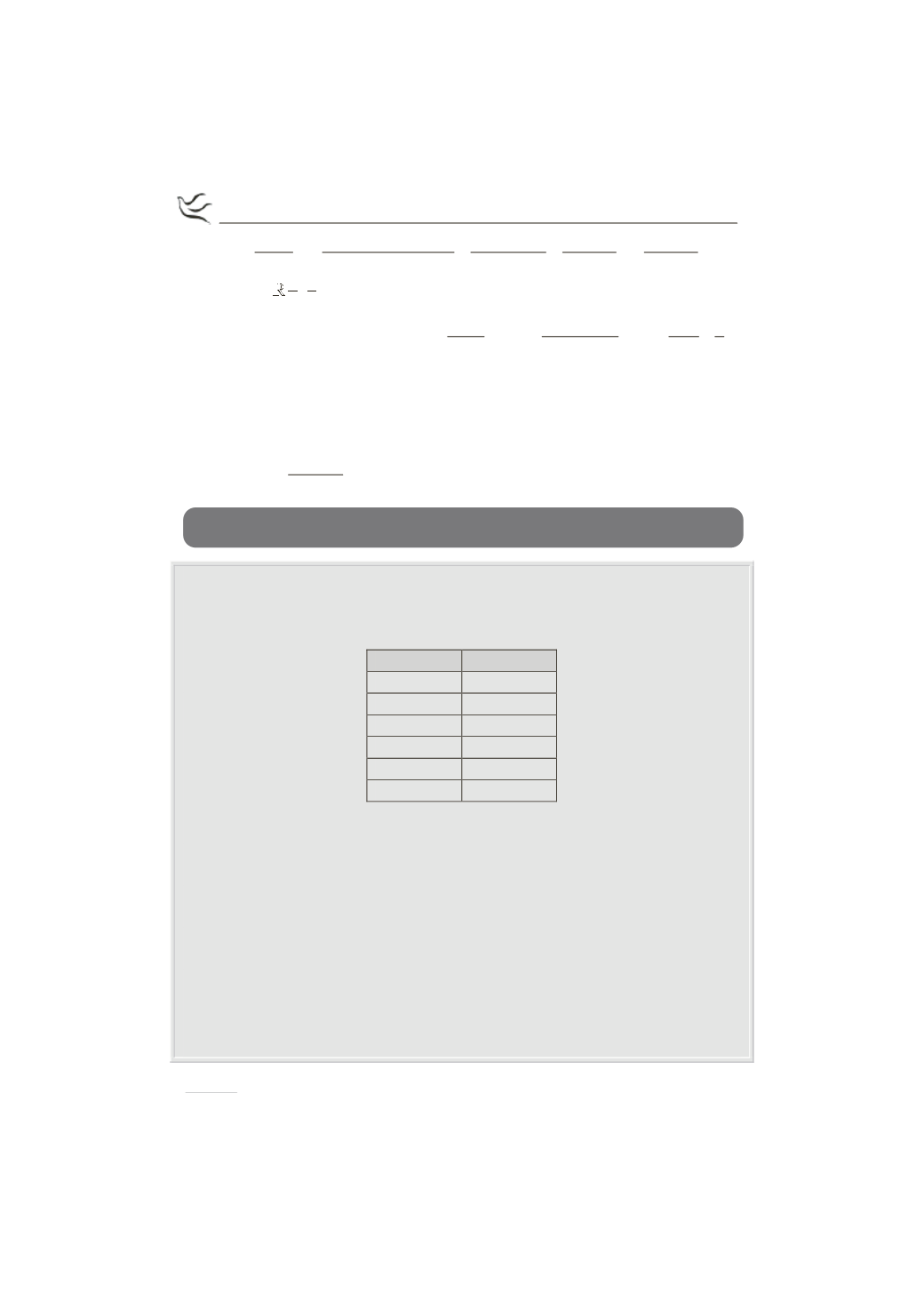
Στον πίνακα που ακολουθεί παρουσιάζεται η χρηματική παροχή από τους
γονείς, σε Ευρώ, δείγματος έξι μαθητών της πρώτης τάξης (ομάδα Α) και έξι
μαθητών της δεύτερης τάξης (ομάδα Β) ενός Γυμνασίου.
Ομάδα Α
Ομάδα Β
1
7
8
14
9
6
5
4
3
12
4
5
α.
Να υπολογίσετε τη μέση τιμή και τη διάμεσο των παρατηρήσεων κάθε
ομάδας.
(
Μονάδες 6
)
β.
Να συγκρίνετε μεταξύ τους ως προς την ομοιογένεια τις δύο ομάδες.
(
Μονάδες 5
)
γ.
Αν σε κάθε παρατήρηση της ομάδας Α γίνει αύξηση 20% και οι
παρατηρήσεις της ομάδας Β αυξηθούν κατά 5 Ευρώ η κάθε μία, πώς
διαμορφώνονται οι νέες μέσες τιμές των δύο ομάδων;
(
Μονάδες 8
)
δ.
Να συγκρίνετε μεταξύ τους ως προς την ομοιογένεια τις δύο ομάδες με τα
νέα δεδομένα.
(
Μονάδες 6
)
ΘΕΜΑ
Δ
ΠΑΝΕΛΛΑΔΙΚΕΣ
ΕΞΕΤΑΣΕΙΣ 200
3









