123
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
·
Συμπληρώνουμε στον πίνακα τις στήλες
i
x
,
i
f
και
i
i
x f
×
:
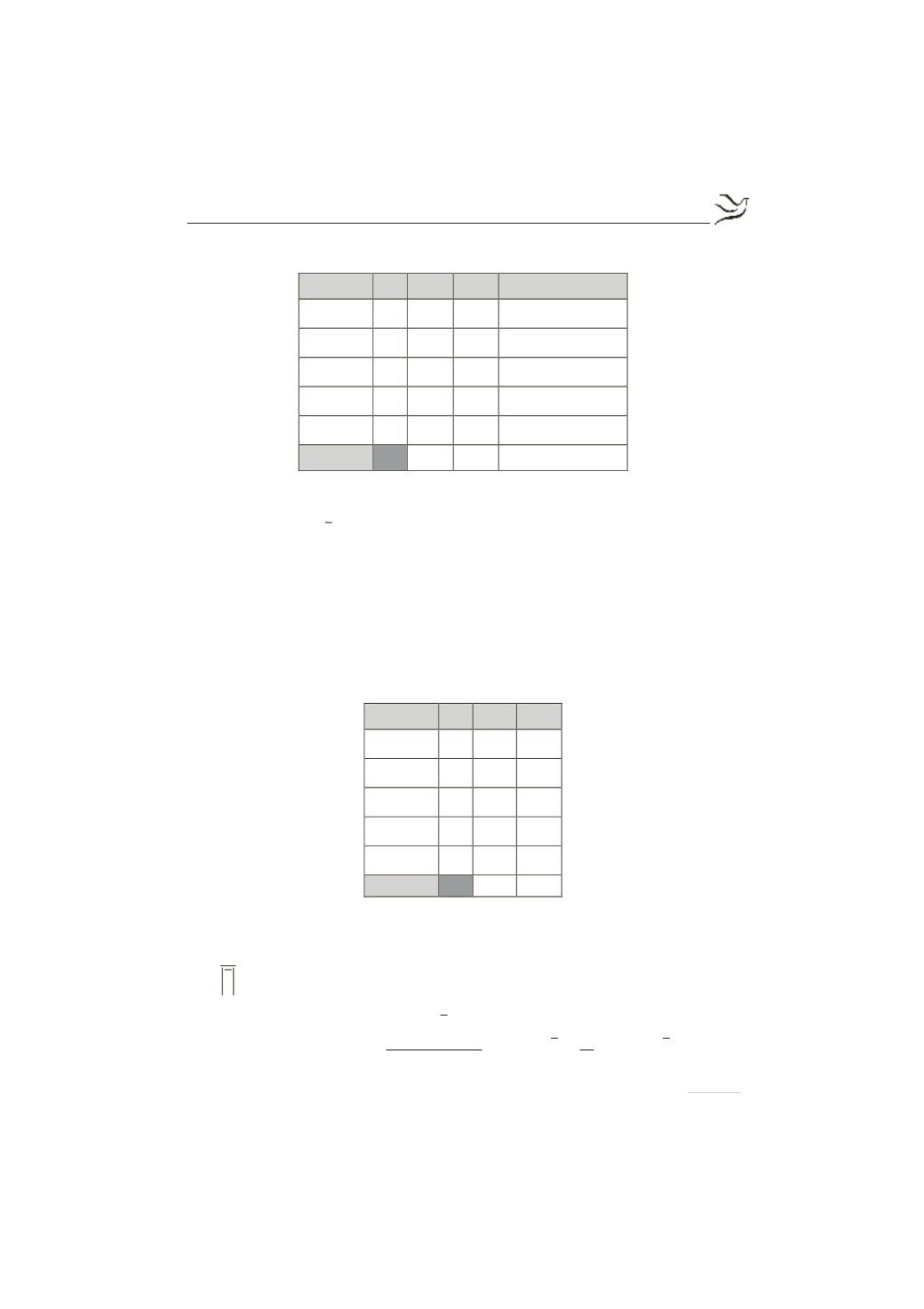
Κλάσεις
i
x
i
f %
i
f
i
i
x f
×
[
)
8,10
9
10
0,1
0,9
[
)
10,12
11
2
f %
2
f
2
11f
[
)
12,14
13 30
0,3
3,9
[
)
14,16
15
4
f %
4
f
4
15f
[
)
16,18
17 30
0,3
5,1
Σύνολα
100
1
2
4
9,9 11f 15f
+ +
Από τα παραπάνω προκύπτει ότι:
2
4
5
2
4
i
i 1
2
4
2
2
2 4
4
4
x 14
9,9 11f 15f 14
0,1 f 0,3 f 0,3 1
f 1
11f 15f 4,1 f 0,1 f % 10
f f 0,3
f 0,2 f % 20
=
ì
ü =
+ + =
ì
ü
ï
ï
Û
Û
í
ý í
ý
+ + + + =
= î
þ
ï
ï
î
þ
+ =
=
=
ì
ü ì
ü ì
ü
Û
Û Û
í
ý í
ý í
ý
+ =
=
=
î
þ î
þ î
þ
å
Τότε ο πίνακας γίνεται:
Κλάσεις
i
x
i
f %
i
f
[
)
8,10
9
10
0,1
[
)
10,12
11 10
0,1
[
)
12,14
13 30
0,3
[
)
14,16
15 20
0,2
[
)
16,18
17 30
0,3
Σύνολα
100
1
Γ2.
Για να εξετάσουμε εάν το δείγμα είναι ομοιογενές, θα χρειαστούμε το
s
CV
x
=
. Εφόσον η μέση τιμή είναι ακέραιος αριθμός, θα υπολογίσουμε τη
διασπορά από τον τύπο
(
)
(
)
(
)
5
2
i
i
5
5
2
2
2 i 1
i
i
i
i
i 1
i 1
x x
ν
ν
s
x x
x x f
ν
ν
=
=
=
- ×
=
= - × = - ×
å
å å
, άρα









