115
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
·
Έχει μέση τιμή
x 8
=
και
·
τυπική απόκλιση
s
, τέτοια ώστε
2
2s 5s 2 0
- + =
τότε
α)
να αποδείξετε ότι
s 2
=
(Μονάδες 4)
β)
να βρείτε τη μέση τιμή των
2
i
x
με
i 1,2,...,15
=
Δίνεται ότι
2
ν
i
ν
i 1
2
2
i
i 1
t
1
s
t
ν
ν
=
=
ì
ü
æ
ö
ï
ï
ç
÷
ï
ï
è
ø
=
- í
ý
ï
ï
ï
ï
î
þ
å
å
(Μονάδες 4)
Δ3.
Επιλέγουμε τυχαία ένα από τα παραπάνω σημεία
(
)
i
i
i
A x ,y
,
i 1,2,...,15
=
. Να βρείτε την πιθανότητα του ενδεχομένου:
(
)
{
}
i
i
i
i
i
B A x ,y , i 1,2,...,15
τέτοια, ώστε y 4x 9R 1
=
=
> - + +
,
όπου
R
είναι το εύρος των
( )
i
i
y E x
=
,
i 1,2,...,15
=
.
(Μονάδες 9)
Απάντηση:
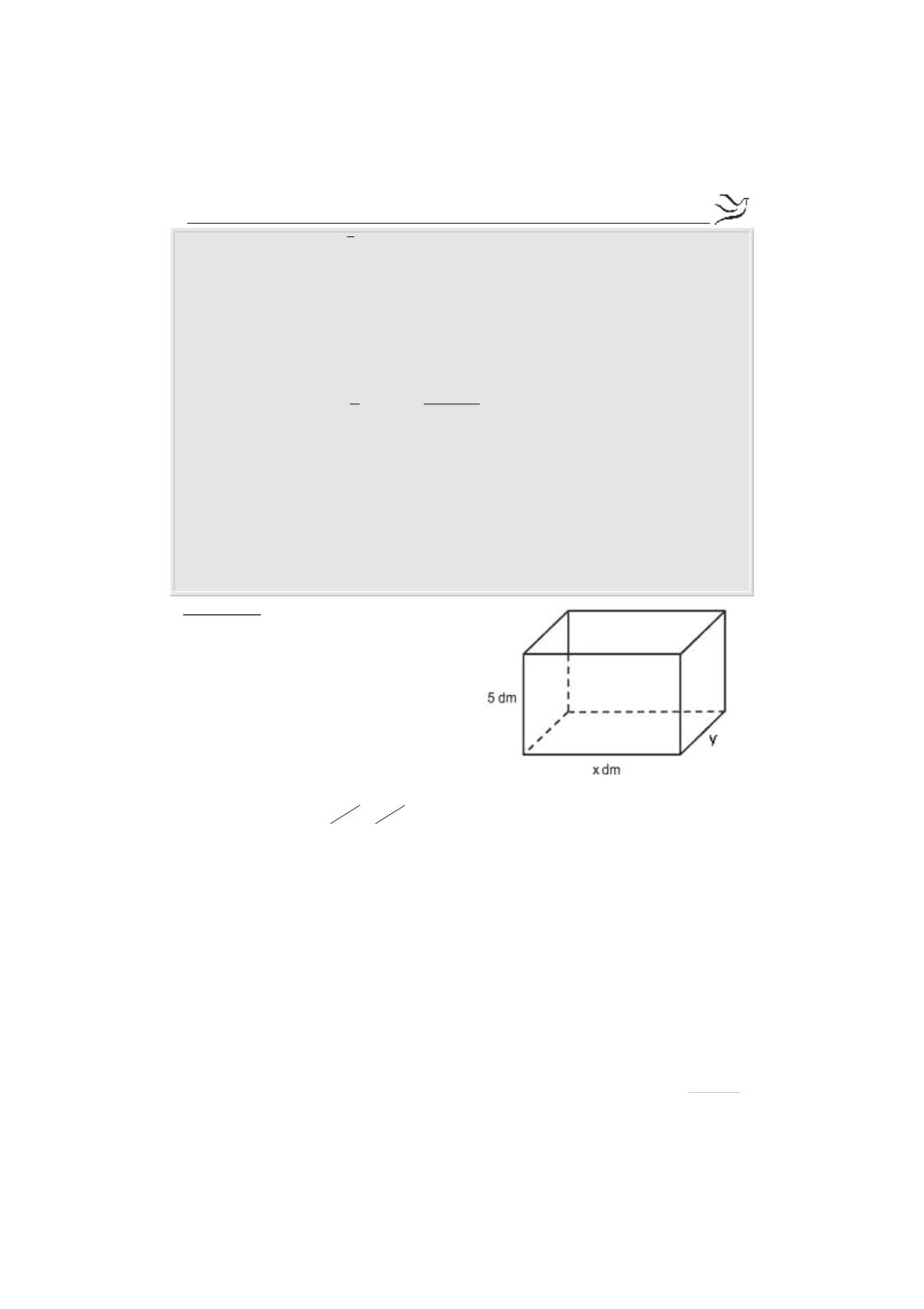
Δ1.
Έστω
y
το πλάτος του ορθογωνίου
της βάσης. Τότε:
2x 2y 20 x y 10 y 10 x
+ = Û + = Û = -
με
(
)
x 0,10
Î
Τότε το συνολικό εμβαδόν είναι ίσο με:
(
)
(
)
2
E x 10 x 2 5 10 x 2 5 x
10x x 100 10x
= ×
- + × ×
- + × × =
= - + -
10x
+
2
x 10x 100
= - + +
Συνεπώς η συνάρτηση που εκφράζει το εμβαδό του κουτιού είναι η:
( )
2
E x x 10x 100
= - + +
με πεδίο ορισμού το
(
)
E
D 0,10
=
.
Θα μελετήσουμε τη συνάρτηση ως προς τα ακρότατα. Είναι:
·
( )
E' x 2x 10
= - +
με
(
)
x 0,10
Î
.
·
( )
E' x 0 2x 10 0 x 5
= Û- + = Û =
.
·
( )
E' x 0 2x 10 0 2x 10 x 5
> Û- + > Û- > - Û <
. Όμως
(
)
x 0,10
Î
, άρα
είναι
( )
( )
E' x
0 x 0,5
> Û Î
.
dm









