Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
114
·
( ) (
) ( ) ( ) (
)
P
Ε P A Π P A P Π P A Π
¢
¢
¢
= È = + - Ç =
( ) (
)
( )
A
Π Α
1
1 5
1 P
Π P A Π
1
P A
3
3 12
- =
= + - -
- = + - - =
1 5 1 5 7
1
1
3 12 3 12 12
= + -
- = - =
.
Γ3.
Είναι
( ) ( )
( )
( )
( )
( )
( ) ( )
( ) ( )
( )
:N
Ω 0
Ν Α Ν Π
4
4
Ν Α Ν Π 4
P Α P Π
Ν Ω Ν Ω Ν Ω
Ν Ω
¹
= - Û = - Û = - Û
( )
( )
( )
( )
1 5 4
4 5 1 4 1
Ν Ω 48
3 12
Ν Ω Ν Ω 12 3 Ν Ω 12
Û = - Û = - Û = Û =
μπάλες
.
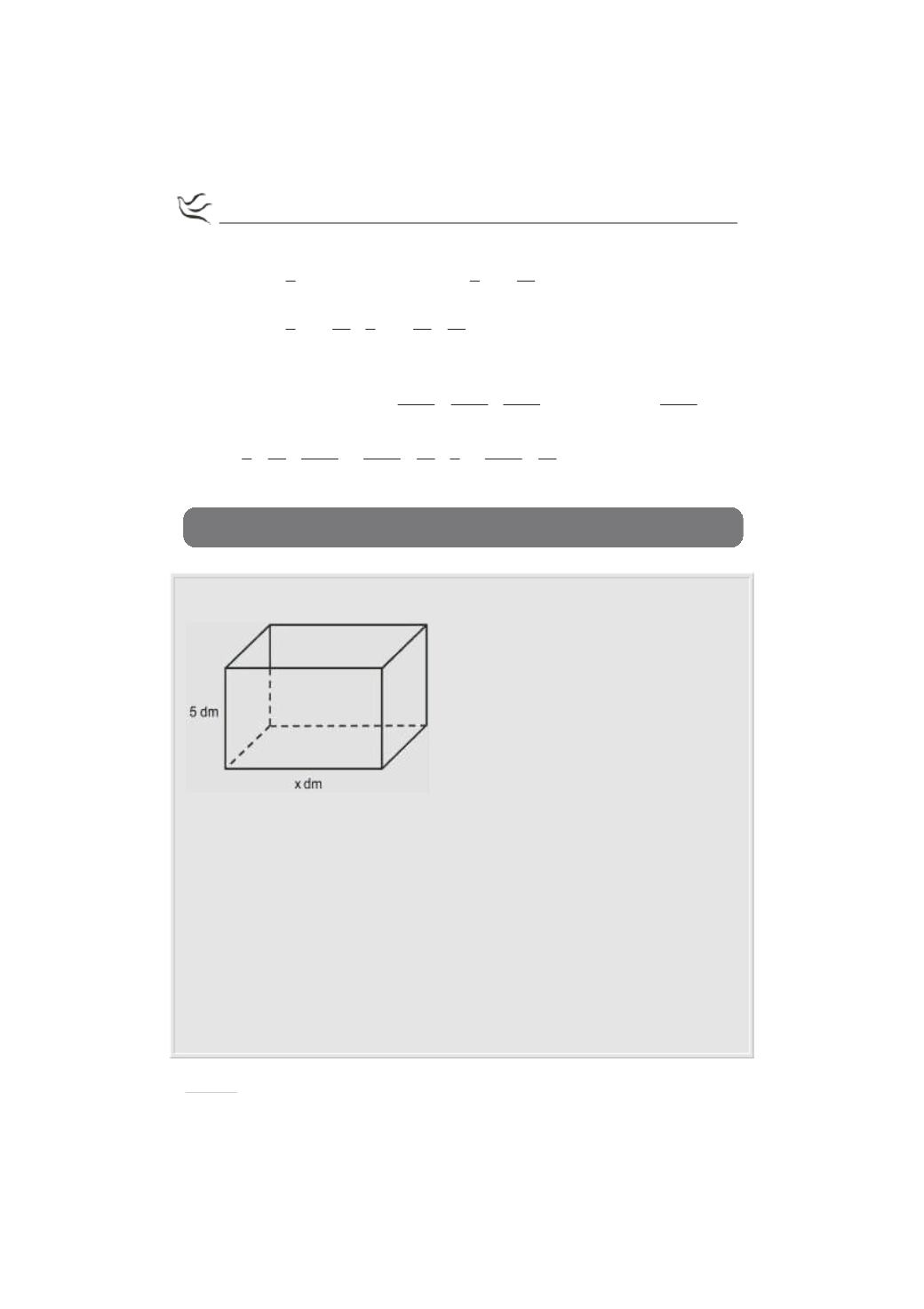
Θεωρούμε ένα κουτί σχήματος ορθογωνίου παραλληλεπιπέδου με βάση
ορθογώνιο και
ανοικτό από πάνω
.
Το ύψος του κουτιού είναι 5 dm.
Η βάση
του κουτιού έχει σταθερή
περίμετρο 20
dm και μία πλευρά της είναι x dm με
0 x 10
< <
.
Δ1.
Να αποδείξετε ότι η συνολική επιφάνεια του κουτιού ως συνάρτηση
του x είναι
:
( )
2
E x x 10x 100
= - + +
,
(
)
x 0,10
Î
και να βρείτε για ποια
τιμή του
x
το κουτί έχει μέγιστη επιφάνεια.
(Μονάδες 8)
Στη συνέχεια θεωρούμε τα σημεία
(
)
i
i
i
A x ,y
, όπου
( )
i
i
y E x
=
,
i 1,2,...,15
=
με
1 2
14 15
5 x x ... x x 9
= < < < < =
.
Δ2.
Αν το δείγμα των τετμημένων
i
x
,
i 1,2,...,15
=
των παραπάνω σημείων
(
)
i
i
i
A x ,y
·
Δεν είναι ομοι
o
γενές
ΘΕΜΑ
Δ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ
2014









