Μαθηματικά Γ' Λυκείου

93 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
92
Γ3. Είναι:
· ( ) 2
x
f x 2xe 2x¢ = - , x Î
· ( ) 2 2
x 2 x
f x 2e 4x e 2¢¢ = + - , xÎ
· ( ) ( ) ( )
2 2 2 2
3 x x 3 x x 2
f x 4xe 8xe 8x e 4xe 3 2x= + + = + , x Î
· ( ) ( ) ( )
2
3 x 2
f x 0 4xe 3 2x 0 x 0= Û + = Û =
· ( ) ( ) ( )
2
3 x 2
f x 0 4xe 3 2x 0 x 0> Û + > Û >
· ( ) ( ) ( )
2
3 x 2
f x 0 4xe 3 2x 0 x 0< Û + < Û <
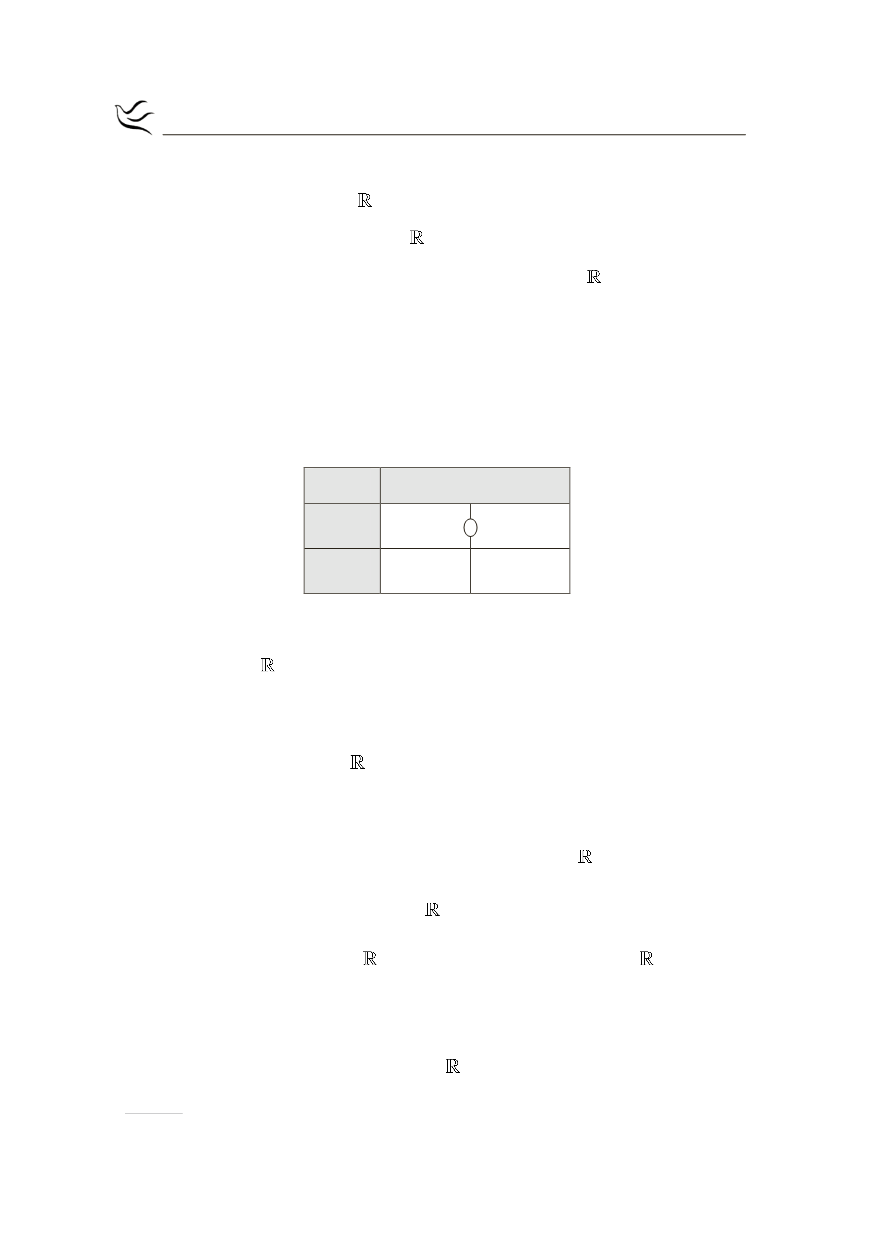
Από τον παραπάνω πίνακα η f¢¢ παρουσιάζει Ολικό Ελάχιστο στο x 0= άρα
για κάθε x Î είναι
( ) ( ) ( )
f x f 0 f x 0¢¢ ¢¢ ¢¢ ³ Û ³ με το «=» μόνο για x 0=
Άρα η f είναι κυρτή στο .
Γ4. Προφανής λύση είναι η x 0=
Θεωρούμε τη συνάρτηση ( ) ( ) ( )
g x f x 3 f x= + - , g D =
Είναι ( ) ( ) ( )
g x f x 3 f x¢ ¢ ¢ = + - , xÎ
Αφού η f είναι κυρτή στο η f΄ είναι γνησίως αύξουσα στο .
Ακόμη ( ) ( ) ( ) ( ) ( ) f
x 3 x f x 3 f x f x 3 f x 0 g x 0
¢
¢ ¢ ¢ ¢ ¢ + > Û + > Û + - > Û >
1
άρα η g είναι γνησίως αύξουσα στο .
x -¥ 0 +¥
( ) ( )
3
f x - +
f¢¢ > <