Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
90
Απάντηση
Γ1.
Η εξίσωση θα λυθεί στο
.
Θεωρούμε τη συνάρτηση
( )
t
h t e t 1
= - -
με
t
Î
.
Η
h
είναι συνεχής στο
ως πραξεις
συνεχών συναρτήσεων και παραγωγί-
σιμη με
·
( )
t
h t e 1
¢
= -
,
t
Î
·
( )
t
t
h t 0 e 1 0 e 1 t 0
¢
= Û - = Û = Û =
·
( )
t
t
h t 0 e 1 0 e 1 t 0
¢
> Û - > Û > Û >
·
( )
t
t
h t 0 e 1 0 e 1 t 0
¢
< Û - < Û < Û <
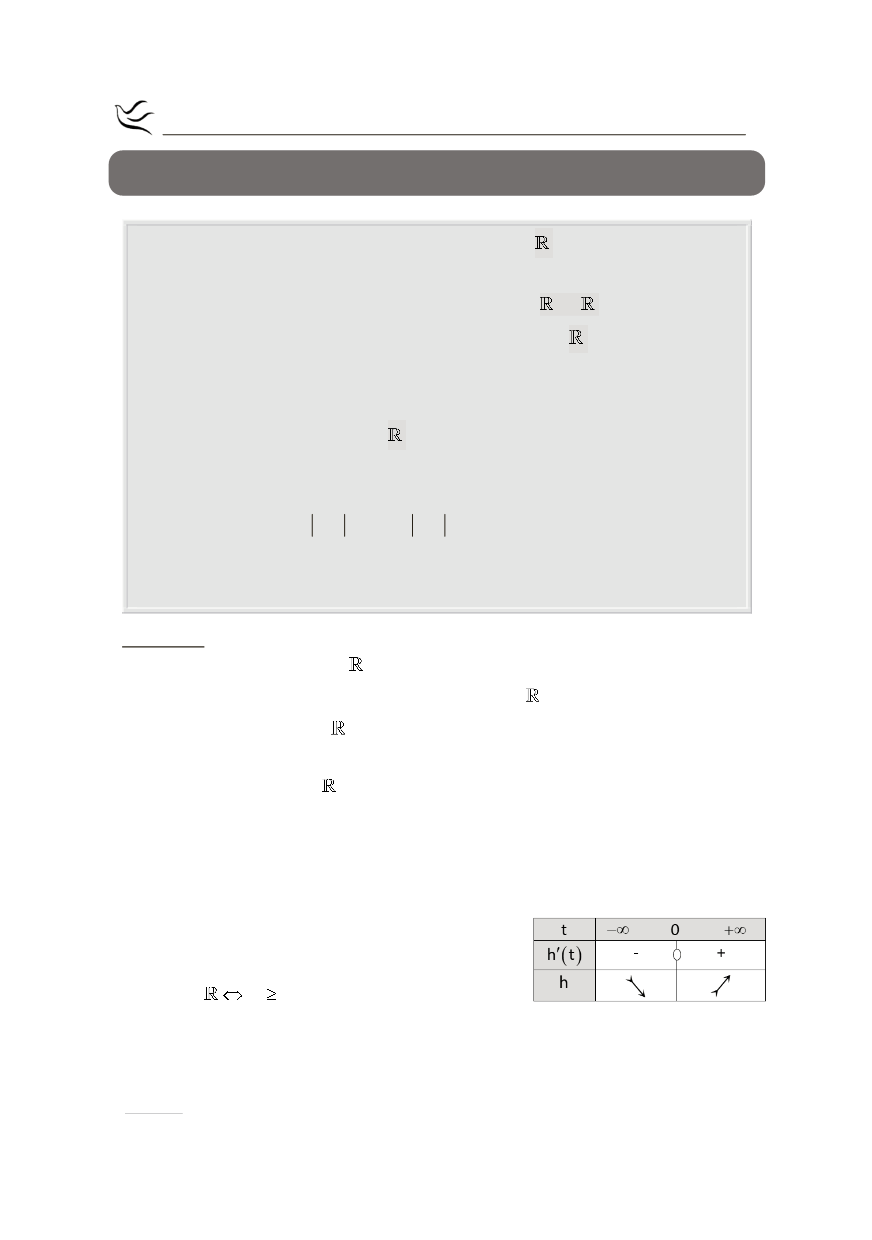
Προκύπτει έτσι ο διπλανός πίνακας μεταβο-
λών
.
Για
[
)
( )
( )
h: 0,
2
2
x
x 0
h x h 0
+¥
Î Û ³ Û ³
1
2
x
2
e x 1 0
Û - - ³
με το «=» μόνο για
x 0
=
άρα η μοναδική λύση της εξίσωσης είναι η
x 0
=
.
Γ1.
Να λύσετε την εξίσωση
2
x
2
e x 1 0, x
- - = Î
.
Μονάδες 4
Γ2.
Να βρείτε όλες τις συνεχείς συναρτήσεις
f :
®
που ικανοποιούν
την σχέση
( )
(
)
2
2
2
x
2
f x e x 1
= - -
για κάθε
x
Î
και να αιτιολογή-
σετε την απάντησή σας.
Μονάδες 8
Γ3.
Αν
2
x
2
f(x) e x 1, x
= - - Î
, να αποδειχθεί ότι η
f
είναι κυρτή.
Μονάδες 4
Γ4.
Αν
f
είναι η συνάρτηση του ερωτήματος
Γ3
, να λυθεί η εξίσωση:
(
) (
)
(
) ( )
f ημx 3 f ημx f x 3 f x
+ -
= + -
όταν
[
)
x 0,
Î +¥
.
Μονάδες 9
ΘΕΜΑ Γ
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 2016









