87
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Β2.
Η συνάρτηση
f
¢
είναι συνεχής στο πεδίο ορισμού της, ως πηλίκο των συνε-
χών συναρτήσεων
( )
3
f x 2x
=
και
( )
(
)
2
2
4
f x x 1
= +
. Επιπλέον, η
f
¢
είναι πα-
ραγωγίσιμη στο , με
·
( )
(
)
( )
(
)
(
)
(
)
2
2
2
2
2
4
2
2
2x x 1 2x x 1
2x
f x
x 1
x 1
¢
¢
¢
é
ù
æ
ö
×
+ - ×
+ ê
ú
ë
û
ç
÷
¢¢
=
=
=
ç
÷ +
+
è
ø
(
)
(
) (
)
(
)
(
)
(
)
(
)
(
) (
)
(
)
(
)
(
)
2
2
2
2
2
2
2 2
4
4
2
2
2
2
2
2
2
2
4
3
3
2
2
2
2 x 1 2x 2 x 1 x 1 2 x 1 8x x 1
x 1
x 1
x 1 2 x 1 8x 2x 2 8x 6x 2
x 1
x 1
x 1
¢
+ - ×
+ ×
+
+ -
+
=
=
=
+
+
é
ù
+ ×
+ -
+ - - +
ë
û
=
=
=
+
+
+
Επιπλέον,
·
( )
(
)
2
2
2
3
2
6x 2
1
1
3
f x 0
0 6x 2 0 x
x
x
3
3
3
x 1
- +
¢¢
= Û = Û - + = Û = Û = ± Û = ±
+
·
( )
(
)
(
)
3
2
x 1 0 για κάθε x
2
2
3
2
6x 2
f x 0
0
6x 2 0
x 1
+ >
Î
- +
¢¢
> Û >
Û - + >
+
2
1
3
3
x
x
3 3
3
Û < Û- < <
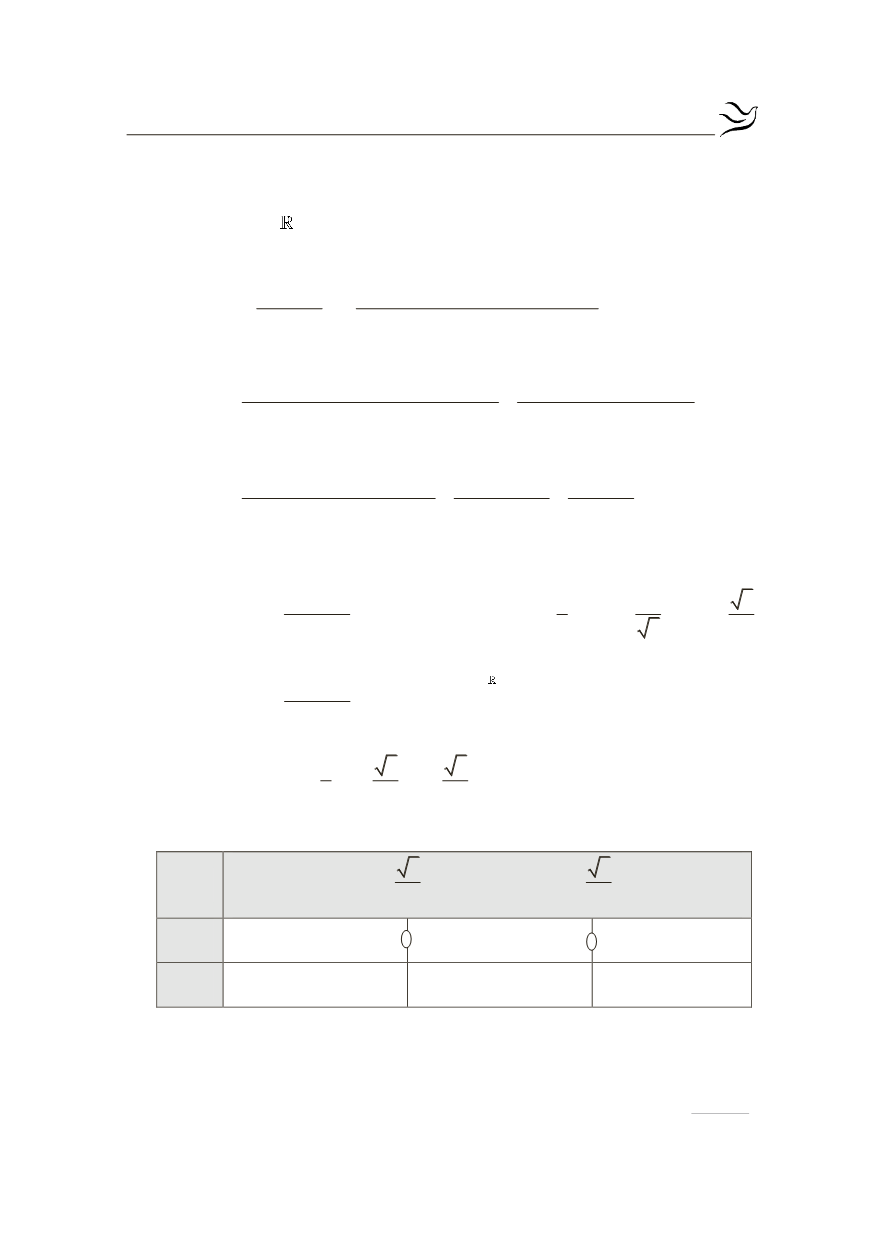
Ακολουθεί ο πίνακας μεταβολών:
x
3
3
3
3
-¥
-
+¥
( )
f x
¢¢
-
+
-
f
4
3
4
ΣΚ
ΣΚ









