Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
84
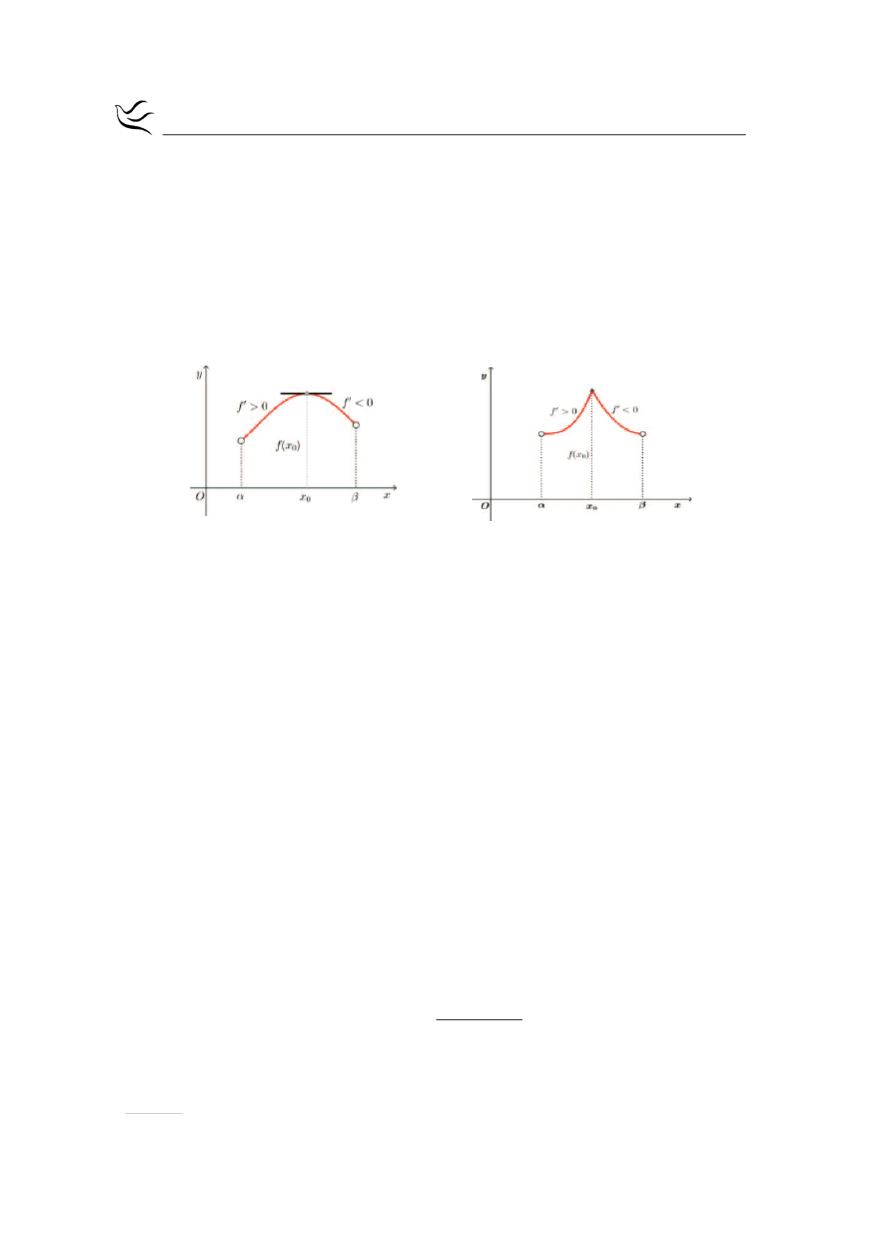
Α1.
Επειδή
( )
f x 0
¢
>
για κάθε
(
)
0
x α,x
Î
και η f είναι συνεχής στο
0
x
, η f είναι
γνησίως αύξουσα στο
(
]
0
α,x
. Έτσι έχουμε
( ) ( )
0
f x f x
£
, για κάθε
(
]
0
x α,x
Î
.
( )
1
Επειδή
( )
f x 0
¢
<
για κάθε
(
)
0
x x ,β
Î
και η f είναι συνεχής στο
0
x
, η f είναι
γνησίως φθίνουσα στο
( )
1
. Έτσι έχουμε:
( ) ( )
0
f x f x
£
, για κάθε
[
)
0
x ,β
.
( )
2
Επομένως, λόγω των
( )
1
και
( )
2
, ισχύει:
( ) ( )
0
f x f x
£
, για κάθε
( )
x α,β
Î
,
που σημαίνει ότι το
( )
0
f x
είναι μέγιστο της f στο
( )
α,β
και άρα τοπικό
μέγιστο αυτής.
Α2.
Δύο συναρτήσεις f και g λέγονται ίσες και γράφουμε
f g
=
όταν:
P
έχουν το ίδιο πεδίο ορισμού Α και
P
για κάθε
x A
Î
ισχύει
( ) ( )
f x g x
=
.
Α3.
Αν μια συνάρτηση
f
είναι :
P
συνεχής στο κλειστό διάστημα
[ ]
α,β
P
παραγωγίσιμη στο ανοικτό διάστημα
( )
α,β
τότε υπάρχει ένα, τουλάχιστον
( )
ξ α,β
Î
τέτοιο ώστε
( ) ( ) ( )
f β f α
f ξ
β α
-
¢
=
-
.









