Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

76 / 146

75
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
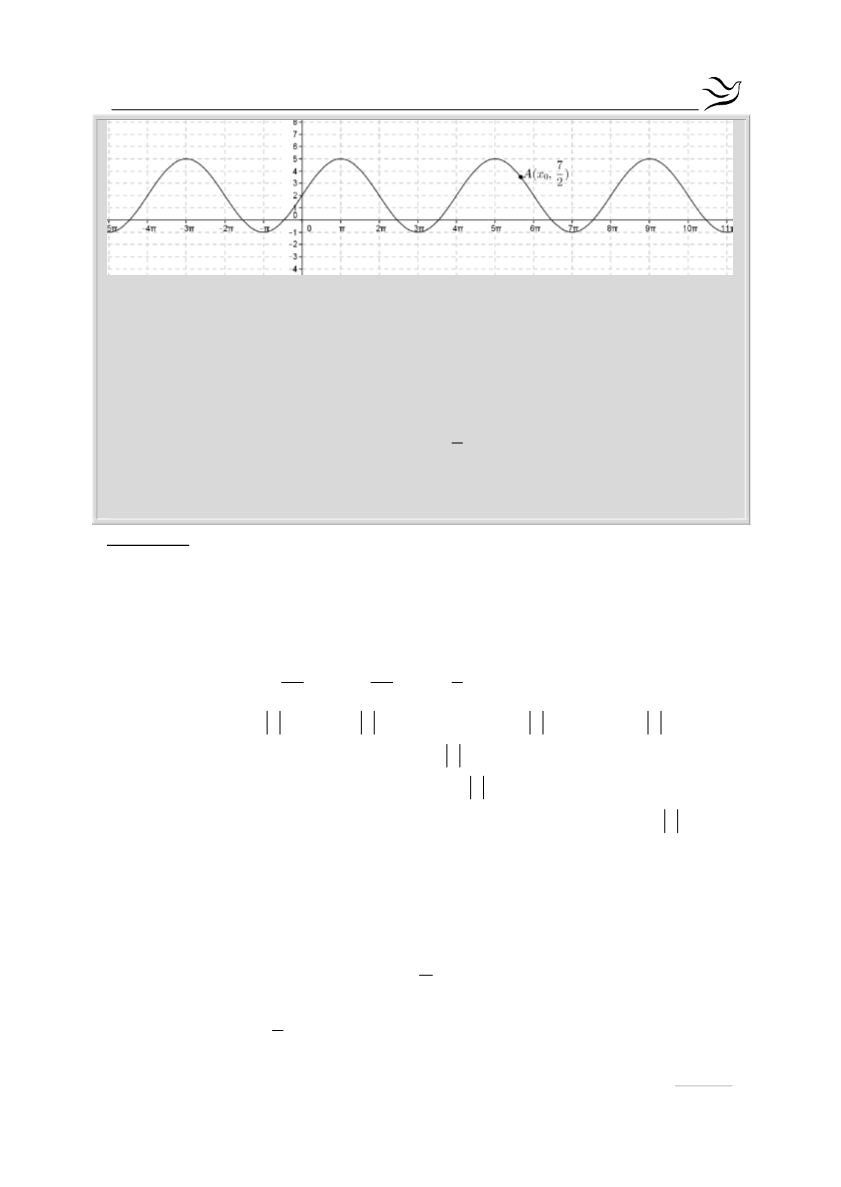
α. Με βάση τη γραφική παράσταση να βρείτε:
i. τη μέγιστη και την ελάχιστη τιμή της συνάρτησης f . (Μονάδες 3)
ii. την περίοδο Τ της συνάρτησης f . (Μονάδες 3)
β. Να προσδιορίσετε τις τιμές των σταθερών ρ,ω και k. Να αιτιολογήσετε
την απάντησή σας. (Μονάδες 9)
γ. Θεωρώντας γνωστό ότι
1
ρ 3,ω 2  και k 2 , να προσδιορίσετε
αλγεβρικά την τετμημένη 0 x του σημείου Α της γραφικής παράστασης
που δίνεται στο σχήμα. (Μονάδες 10)
Απάντηση:
α. Από τη γραφική παράσταση παρατηρούμε ότι η μέγιστη τιμή της
συνάρτησης είναι max f 5  και η ελάχιστη min f 1  
Εύκολα διακρίνουμε ότι η συνάρτηση παίρνει μέγιστη τιμή στο 1 x π
και μετά ξανά στο 2 3 x 5π,x 9π   κ.ο.κ, άρα η περίοδος είναι Τ 4π .
β. Έχουμε ότι:
2π 2π 1
Τ 4π ω
ω ω 2
     .
Επίσης: max f ρ k 5 ρ k       1 και min f ρ k 1 ρ k         2
Συνεπώς προκύπτει το σύστημα:
5 ρ k
1 ρ k
   

    
με πρόσθεση κατά μέλη έχουμε: 2k 4 k 2   άρα από  1  ρ 3  .
Τέλος από τη γραφική παράσταση παρατηρούμε ότι η συνάρτηση είναι
γνησίως αύξουσα στο διάστημα   0,π που σημαίνει ότι ρ 0 , άρα ρ 3 .
Εναλλακτικά μπορούμε να επικαλεστούμε ότι διέρχεται από το σημείο
  Β π,5 το οποίο μας δίνει ότι:
 
π
f π 5 ρ ημ 2 5 ρ 3
2
 
      
 
 
.
γ. Εφόσον 0 f
7
Α x , C
2
 
 

 
έχουμε ότι: