Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

69 / 146

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου
68
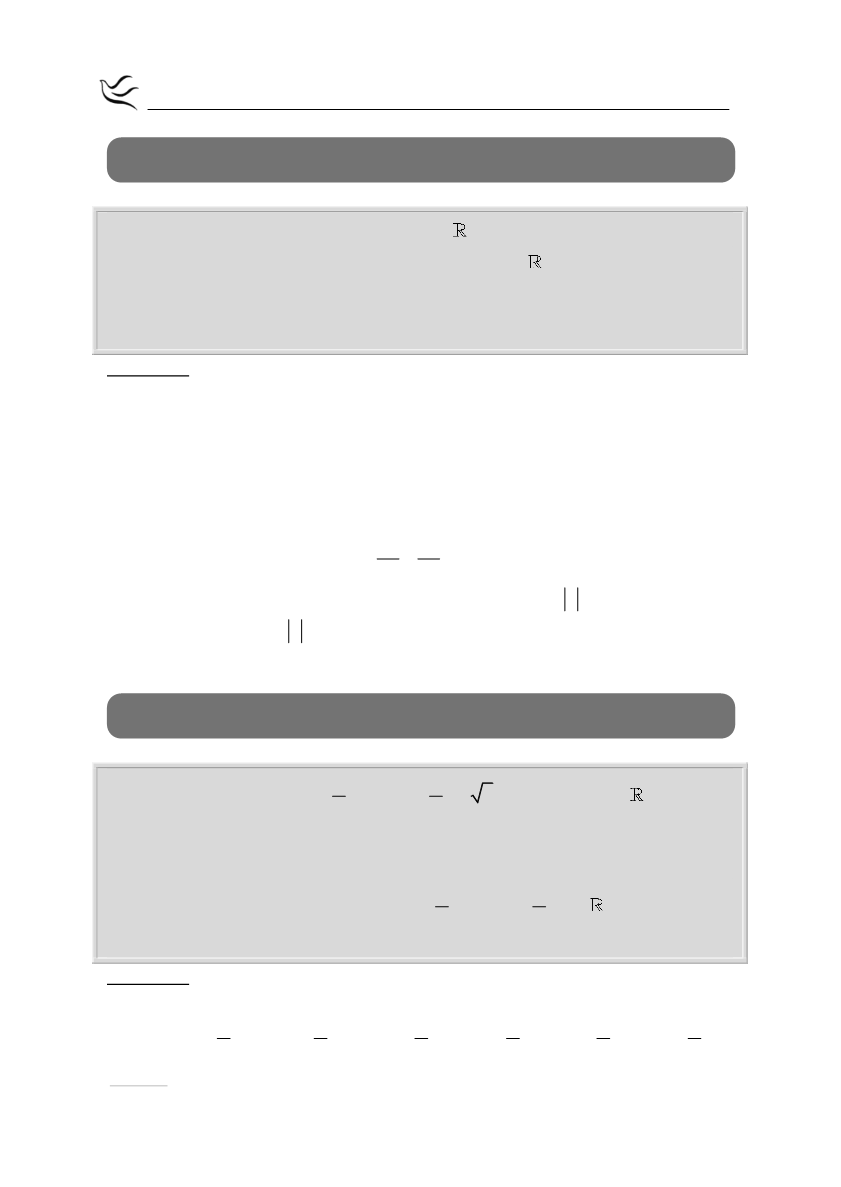
Έστω η συνάρτηση    2
f x ημx συνx   , x  .
α. Να αποδείξετε ότι   f x 1 ημ2x  για κάθε x  .
(Μονάδες 12)
β. Να βρείτε την περίοδο καθώς και τη μέγιστη και ελάχιστη τιμή της f .
(Μονάδες 13)
Απάντηση:
α. Έχουμε ότι:
   2 2 2 f x ημx συνx ημ x 2ημxσυνx συν x    
Γνωρίζουμε όμως ότι: 2 2 ημ x συν x 1   1 και ημ2x 2ημxσυνx  2 .
Άρα με την βοήθεια των    1 & 2 η f παίρνει τη μορφή
  f x 1 ημ2x   .
β. Η περίοδος της f είναι:
2π 2π
T π
ω 2
  
Η μέγιστη τιμή της συνάρτησης θα είναι: max f p c 1 1 2      και η
ελάχιστη min f p c 1 1 0        .
α. Να δείξετε ότι
π π
ημ x ημ x 2ημx
4 4
   
   
   
   
για κάθε x  .
(Μονάδες 13)
β. Να βρείτε με τη βοήθεια του ερωτήματος   α τη μέγιστη και ελάχιστη
τιμή της συνάρτησης  
π π
f x ημ x ημ x ,x
4 4
   
       
   
.
(Μονάδες 12)
Απάντηση:
α. Έχουμε ότι:
π π π π π π
ημ x ημ x ημxσυν συνxημ ημxσυν συνxημ
4 4 4 4 4 4
   
       
   
   
ΘΕΜΑ 57. 2-19913
ΘΕΜΑ 58. 2-22639