Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου
140
γ.
Για την ανίσωση έχουμε:
f x x 3ln2
x
ln e
2
x 3ln2
2x
x
e
2e
8 0
και πάλι για
x
e t
καταλήγουμε στο:
2
t
2t 8 0
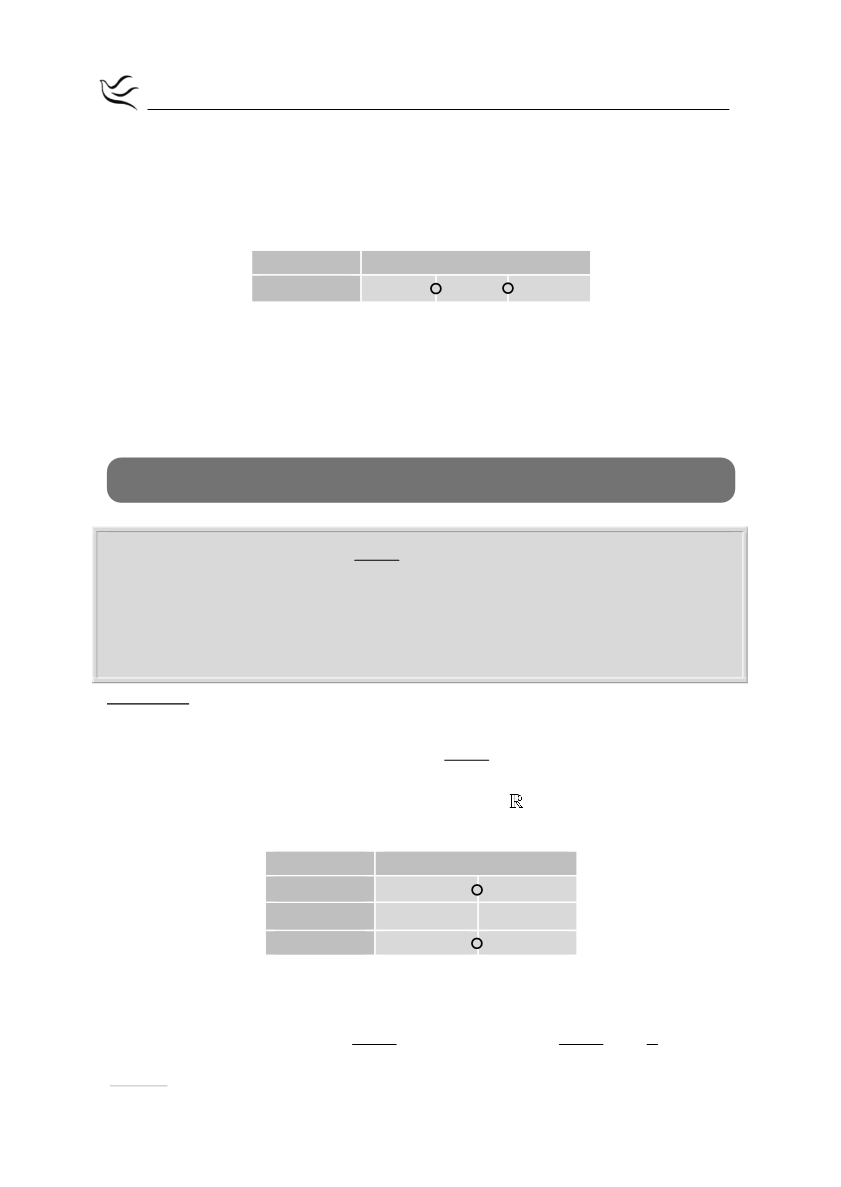
Από τον πίνακα προσήμων έχουμε:
t
2 4 +
2
t 2t 8
+
-
+
συνεπώς:
t
2
ή
t 4
x
e
2
ή
x
e 4
αδύνατο διότι
x
e
0
ή
x
ln4
Άρα
x ln4,
.
Δίνεται η συνάρτηση
x
x
4 1
f x
log
.
2 5
α.
Να βρείτε το πεδίο ορισμού της f. (Μονάδες 7)
β.
Να λύσετε την εξίσωση
f x
log3 log7.
(Μονάδες 9)
γ.
Να λύσετε την ανίσωση
f x
log3 log7.
(Μονάδες 9)
Απάντηση
:
α.
Για να ορίζεται η
f
θα πρέπει:
x
2
5 0
1
και
x
x
4
1
0
2
5
2
για την
1
έχουμε ότι
x
2 5 0
άρα
x
για την
2
από τον πίνακα προσήμων έχουμε:
0 +
x
4
1
-
+
x
2 5
+
+
-
+
Άρα
f
D 0,
.
β.
Έχουμε:
f x log3 log7
x
x
4 1
log
log3 log7
2
5
x
x
4 1
3
log
log
2 5 7
ΘΕΜΑ 118.
4-22812









