113
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
β.
Για
α 1
και
β 0
το πολυώνυμο γίνεται:
3
P x
x
7x 6
.
i. Έχουμε:
3
P x
0 x 7x 6 0
Για το πολυώνυμο έχουμε από το
α
ερώτημα ότι το
x 1
είναι μία ρίζα
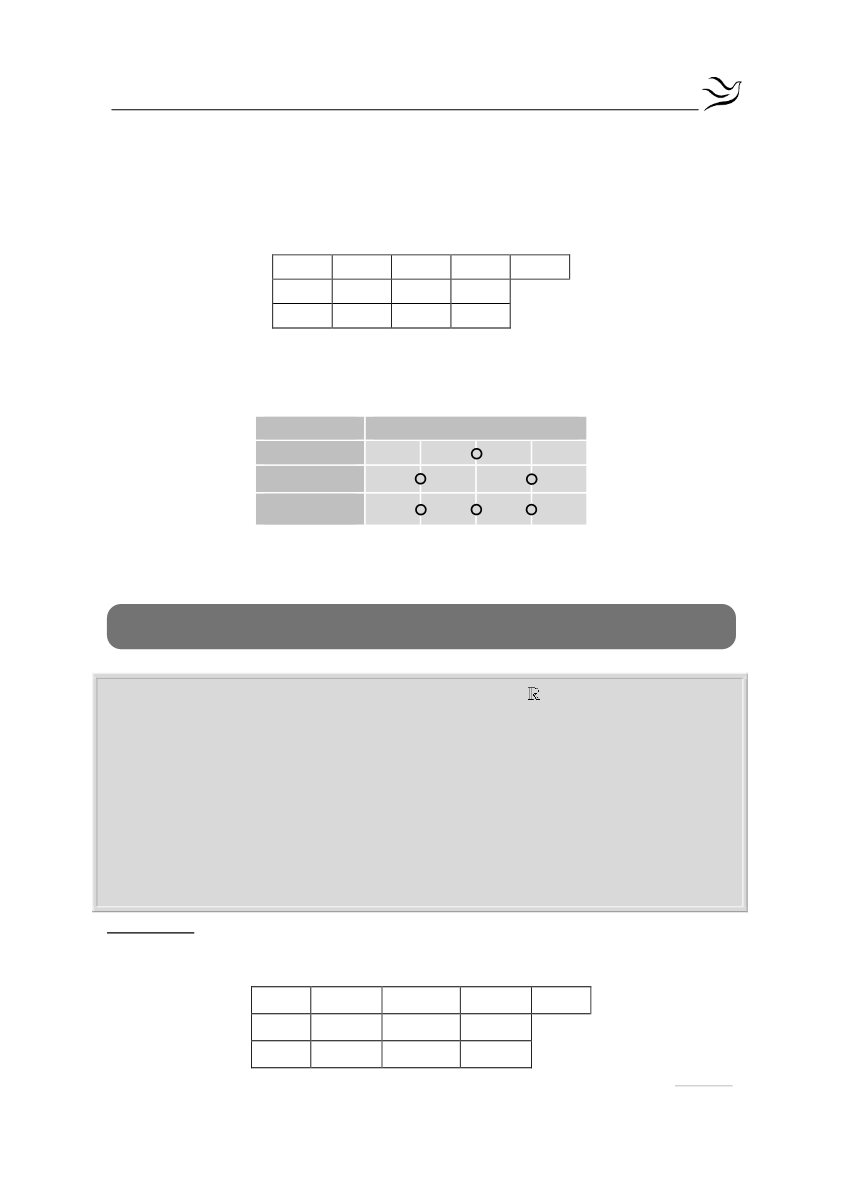
του, οπότε με την βοήθεια του σχήματος Horner η ανίσωση γίνεται:
1
0
-7
6
1
1
1
-6
1
1
-6
0
3
2
x
7x 6 0 x 1 x x 6 0
Για
2
x x 6 0
έχουμε
x 2
ή
x
3
.
Στη συνέχεια, από τον πίνακα προσήμων βλέπουμε ότι:
3 1 2 +
x 1
-
-
+
+
2
x
x 6
+
-
-
+
P x
-
+
-
+
Άρα
x 3,1
2,
.
Δίνεται το πολυώνυμο
3
3 2
2
P x
x α x
α x α
,
α
.
α.
Να κάνετε την διαίρεση
P x : x α
και να γράψετε την ταυτότητα της
διαίρεσης. (Μονάδες 7)
β.
Να βρείτε τις τιμές του α για τις οποίες το
x α
διαιρεί το
P x
.
(Μονάδες 6)
γ.
Αν
α 1
, τότε:
i. Να λύσετε την ανίσωση
P x 0
(Μονάδες 6)
ii. Να λύσετε την ανίσωση
x 1 P x
0
(Μονάδες 6)
Απάντηση:
α.
Η διαίρεση με το
x α
μπορεί να πραγματοποιηθεί με τη βοήθεια του
σχήματος Horner για
ρ α
.
1
3
α
2
α
α
α
α
4
2
α
α
5
α
1
3
α
α
4
α
5
α
α
ΘΕΜΑ 94.
4-22774









