Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

110 / 146

109
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
2 1 2 +    
x 1 - - + +
2 x 2  + - - +
  P x - + - +
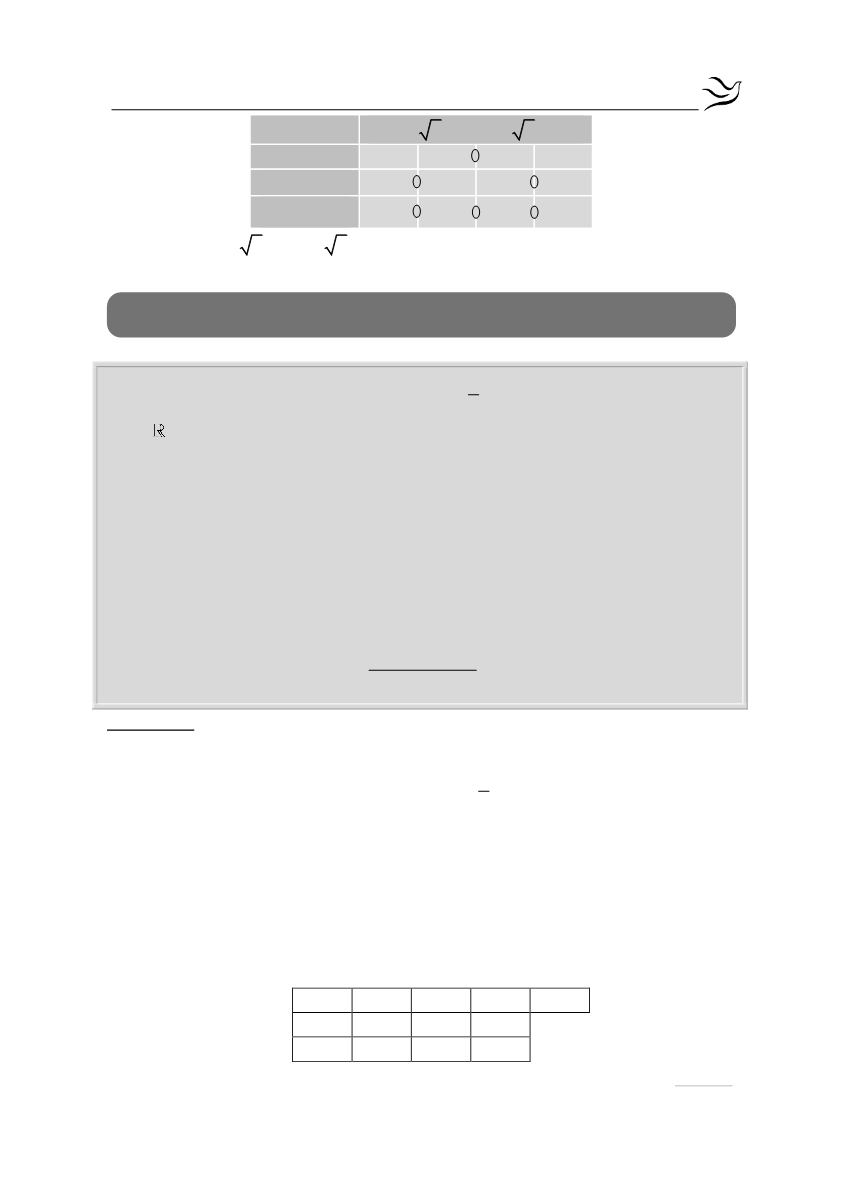
Άρα    
x 2 , 1 2 ,      .
Δίνεται το πολυώνυμο         2 4 3 2 1
P x κ 1 x κ 1 x κ 1 x 3κx λ
2
        με
κ, λ .
α. Να υπολογίσετε τις τιμές των κ και λ αν το πολυωνύμο   P x είναι 3 ου
βαθμού και το υπόλοιπο της διαίρεσης του   P x με το x 1 είναι ίσο με
4  . (Μονάδες 7)
β. Για κ 1 και λ 2 
i. να γράψετε την ταυτότητα της Ευκλείδειας διαίρεσης του πολυωνύ-
μου   P x με το x 1 . (Μονάδες 5)
ii. να λύσετε την εξίσωση   2
P x 4 x 1   . (Μονάδες 7)
iii. να λύσετε την ανίσωση
 
    2
P x
1
x 1 x 2

 
. (Μονάδες 6)
Απάντηση:
α. Εφόσον το   P x είναι 3 ου βαθμού θα έχουμε ότι:
2 κ 1 0   και   1
κ 1 0
2
 
κ 1 ή κ 1  και κ 1  
άρα κ 1 . Συνεπώς το πολυώνυμο παίρνει τη μορφή:   3
P x x 3x λ   .
Γνωρίζουμε επίσης ότι το υπόλοιπο της διαίρεσης του   P x με το   x 1
είναι ίσο με 4  άρα θα ισχύει:   P 1 4    3
1 3 1 λ 4     
2 λ 4 λ 2         , επομένως   3
P x x 3x 2    .
β. i. Από το σχήμα Horner έχουμε:
1 0 -3 -2 1
1 1 -2
1 1 -2 -4
ΘΕΜΑ 91. 4-22766