Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

106 / 146

105
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
β. Θεωρώντας τώρα δεδομένο ότι   3 1
f x x x
4
  :
i. Να αποδείξετε ότι     f x f x    για κάθε x  . (Μονάδες 5)
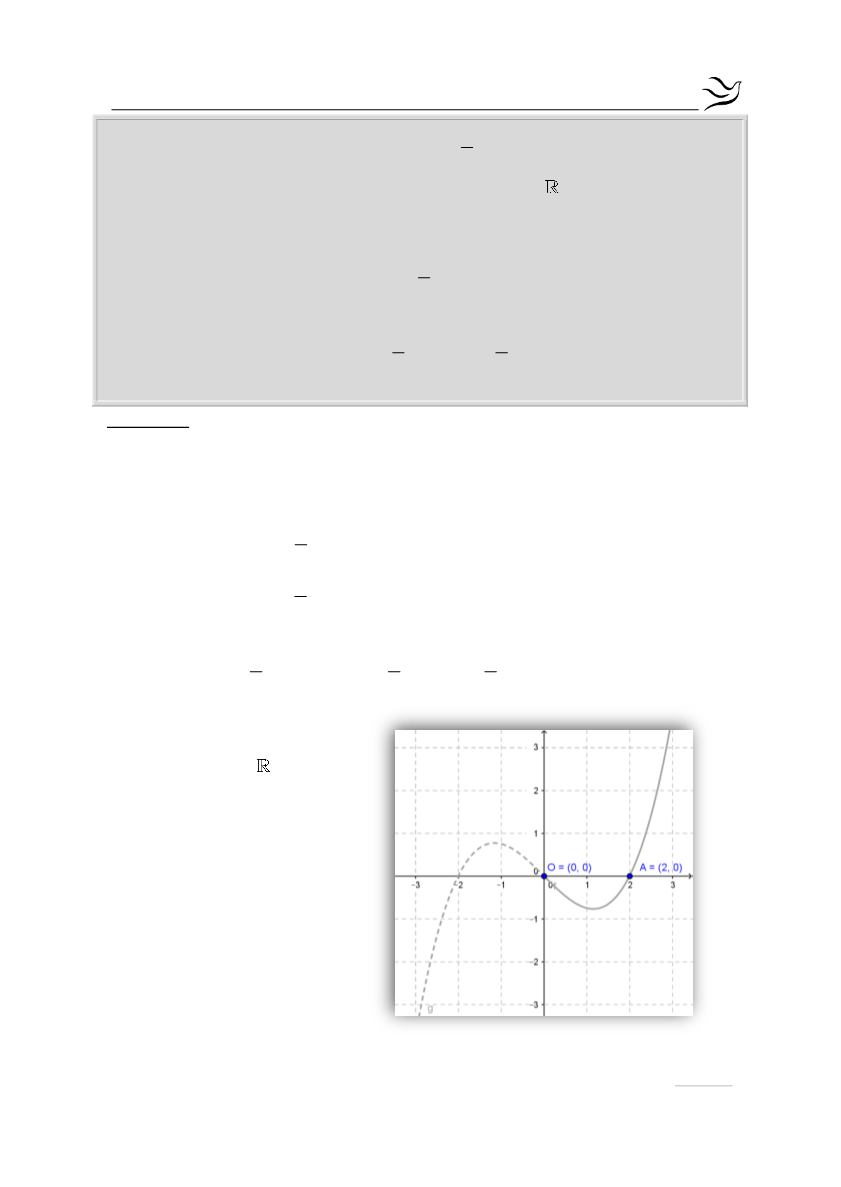
ii. Να μεταφέρετε στην κόλα σας το σχήμα και να συμπληρώσετε τη
γραφική παράσταση της f για x 0 . (Μονάδες 5)
γ. Να επαληθεύσετε ότι  
3
f 1
4
  και στη συνέχεια να λύσετε τις
εξισώσεις:
  3
f x
4
  και   3
f x
4

(Μονάδες 10)
Απάντηση:
α. Από τη γραφική παράσταση βλέπουμε ότι η συνάρτηση διέρχεται από τα
σημεία   O 0,0 και   A 2,0 . Αυτό σημαίνει ότι ισχύει:
  f 0 0  1 και   f 2 0  2
από     3 1
1 f 0 0 γ 0 δ δ 0
4
      
από     3 1
2 f 2 2 2γ 0 0 2 2γ γ 1
4
         
β. Έχουμε:
i.         3 3 3 1 1 1
f x x x x x x x f x
4 4 4
 
             
 
ii. Εφόσον ισχύει
    f x f x   για
κάθε x  , έχουμε
ότι η f είναι περιττή
συνάρτηση, που
σημαίνει ότι η
γραφική της
παράσταση θα έχει
ως κέντρο
συμμετρίας την αρχή
των αξόνων.
Άρα η γραφική της
παράσταση θα έχει
τη μορφή: