Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

105 / 146

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου
104
 
2
2 2 60
x 1 x
x
 
   
 
 
2 2
2
3600
x 2x 1 x
x
    
4 3 2 4 x 2x x x 3600      3 2 2x x 3600 0    .
γ. Παρατηρούμε ότι το x 12 είναι μία λύση της εξίσωσης. Άρα οι άλλες
πλευρές του τριγώνου θα είναι:
  ΒΓ 13 και   60
ΑΓ 5
12
  .
δ. Για να βρούμε αν υπάρχουν κι άλλα τρίγωνα που να ικανοποιούν τα
αρχικά δεδομένα, αρκεί να λύσουμε την εξίσωση 3 2 2x x 3600 0    .
Έτσι, από το σχήμα Horner θα έχουμε:
2 1 0 -3600 12
24 300 3600
2 25 300 0
συνεπώς η εξίσωση τώρα γίνεται:
    2 x 12 2x 25x 300 0     
και για 2
2x 25x 300   προκύπτει Δ 625 2400 1775 0      .
Άρα δεν υπάρχει άλλο τρίγωνο, που να ικανοποιεί τις αρχικές υποθέσεις.
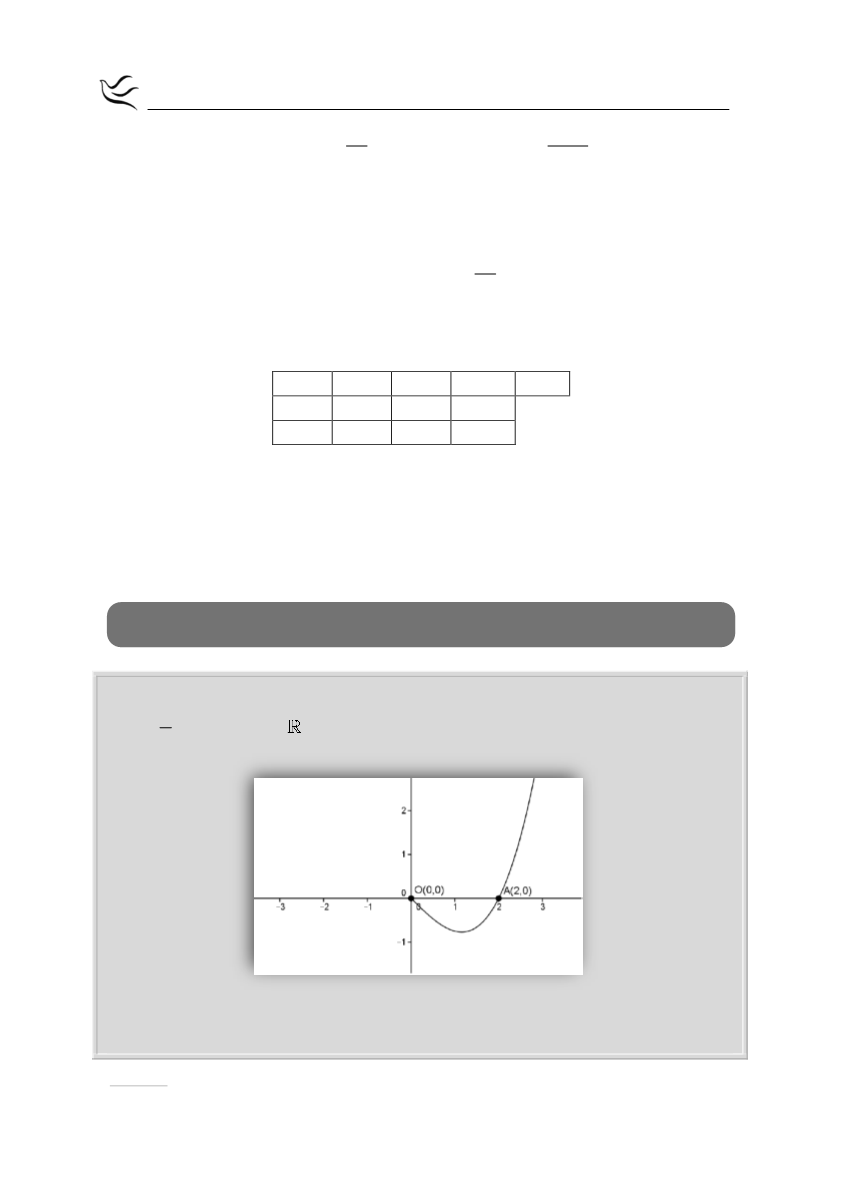
Στο παρακάτω σχήμα δίνεται τμήμα της γραφικής παράστασης της συνάρτησης
  3 1
f x x γx δ
4
   , x  και γ,δ πραγματικές σταθερές
.
α. Με βάση τη γραφική παράσταση, να αποδείξετε ότι γ 1  και δ 0
(Μονάδες 5)
ΘΕΜΑ 88. 4-22759