99
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
γ.
2
P x 0 x 2 x 1 0
, από τον πίνακα προσήμων θα έχουμε ότι:
-1
x 1
-
+
2
x
2
+
+
P x
-
+
Άρα
x
, 1
.
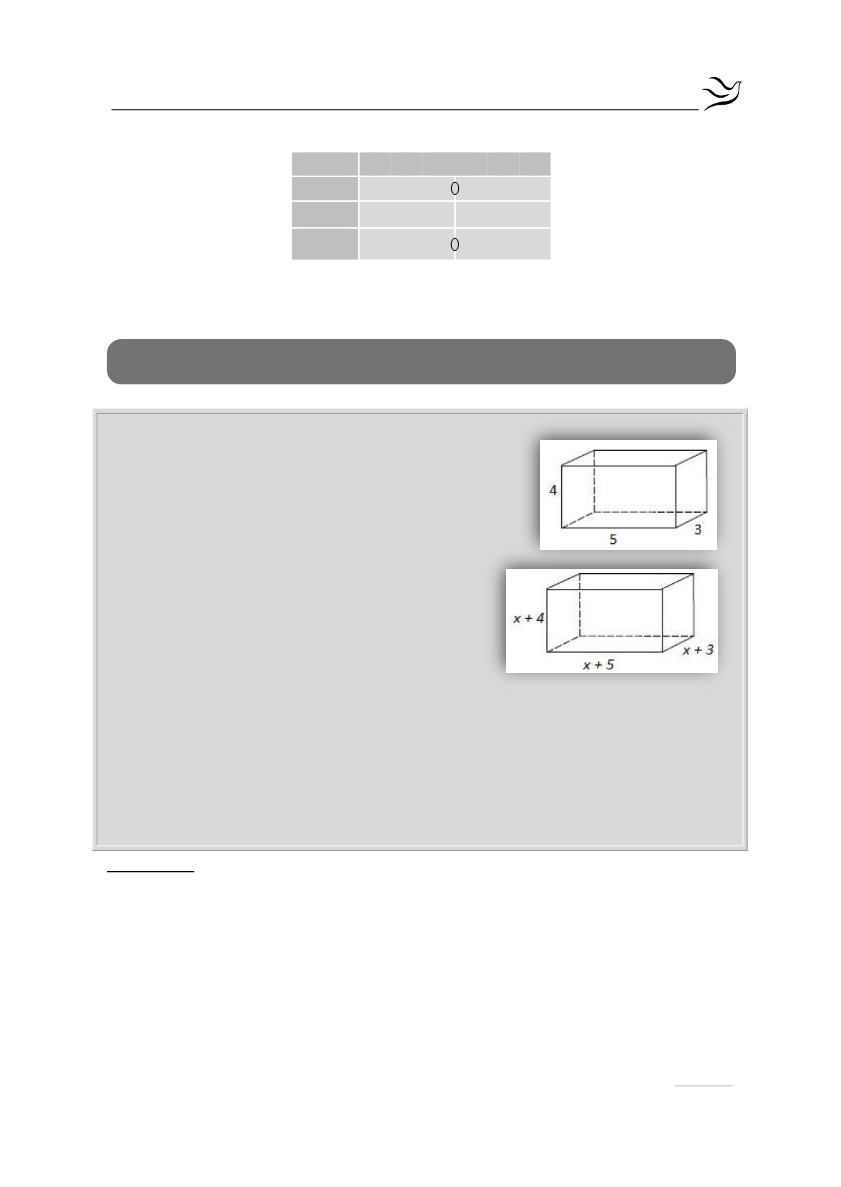
Μια εταιρεία κατασκευάζει κουτιά σχήματος
ορθογωνίου παραλληλεπιπέδου με διαστάσεις
3cm, 4cm και 5cm. Ένας νέος πελάτης ζήτησε από
την εταιρεία να κατασκευάσει κουτιά με όγκο
120
3
cm
, δηλαδή διπλάσιο από εκείνον που
κατασκευάζει. Η εταιρεία αποφάσισε να
κατασκευάσει τα κουτιά που ζήτησε ο
πελάτης της, αυξάνοντας τις διαστάσεις του
αρχικού κουτιού κατά σταθερό ακέραιο
μήκος x .
α.
Να αποδείξετε ότι το x θα είναι λύση της εξίσωσης:
3
2
x
12x 47x 60 0
.
(Ο όγκος V ορθογωνίου παραλληλεπιπέδου με διαστάσεις α, β, γ δίνεται
από τον τύπο:
V α β γ
) (Μονάδες 12)
β.
Να βρείτε τον θετικό ακέραιο x λύνοντας την εξίσωση που δίνεται στο
ερώτημα α). (Μονάδες 13)
Απάντηση:
α.
Ο όγκος του ορθογωνίου παραληλλεπιπέδου ισούται με:
V
x 3 x 4 x 5
2
3
2
2
V x 7x 12 x 5
x 5x 7x 35x 12x 60
3
2
V x
x 12x
47x 60
.
Όμως θέλουμε ο όγκος του κουτιού να είναι 120
3
cm
, άρα:
3
2
V x 120
x
12x
47x 60 120
ΘΕΜΑ 82.
2-22684









