Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

95 / 146

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου
94
.
β. Η f C θα τέμνει τον y΄y για x 0  συνεπώς:
  f 0 6 άρα τέμνει τον y΄y στο σημείο   A 0,6
Θα τέμνει επίσης τον x΄x για   f x 0  4 3 2
2x x 14x 5x 6 0       1
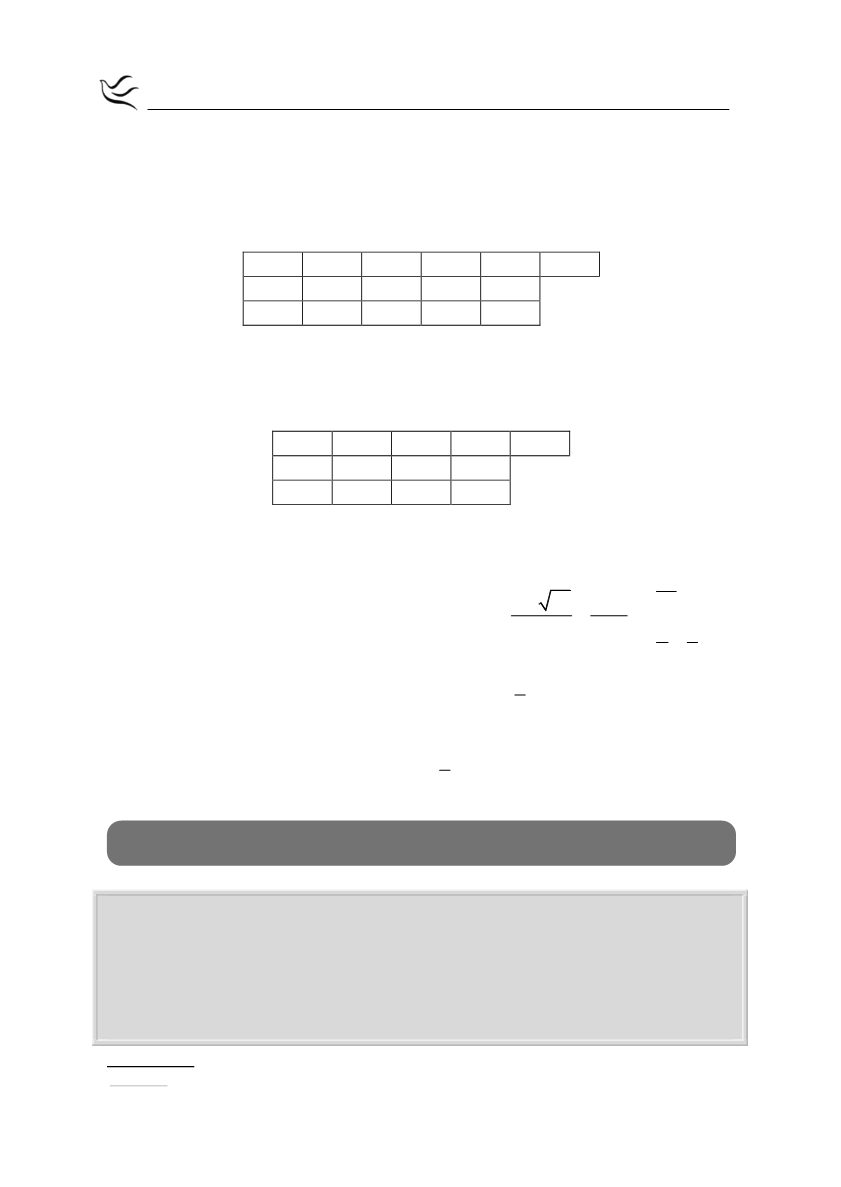
Έχουμε ότι το x 2  είναι ρίζα της f άρα από το σχήμα Horner έχουμε:
2 -1 -14 -5 6 -2
-4 10 8 -6
2 -5 -4 3 0
άρα η εξίσωση γίνεται:
   
3 2
x 2 2x 5x 4x 3 0      2
Παρατηρούμε ότι το 1  είναι ρίζα του τριτοβάθμιου πολυωνύμου, οπότε
και πάλι με την βοήθεια του σχήματος Horner έχουμε:
2 -5 -4 3 -1
-2 7 -3
2 -7 3 0
και η εξίσωση τώρα παίρνει τη μορφή:
    
2
x 2 x 1 2x 7x 3 0     
Τέλος: 2
Δ 7 4 2 3 49 24 25        και 1,2
12
3
7 25 7 5 4
x
2 1 2 2 4
4 2

 
  
   
  

Άρα οι ρίζες της f είναι:
1
x 2,x 1,x
2
     και x 3 και τα σημεία
τομής της γραφικής παράστασης με τον άξονα x΄x είναι τα:
   
1
M 2,0 ,N 1,0 ,K ,0
2
 
   
 
και   Λ 3,0
Δίνεται το πολυώνυμο   3 2 P x 3x 10x 9x 2     .
α. Να κάνετε τη διαίρεση του πολυωνύμου   P x με το πολυώνυμο
2 3x 4x 1  και να γράψετε την ταυτότητα της ευκλείδειας διαίρεσης.
(Μονάδες 15)
β. Να βρείτε τις ρίζες της εξίσωσης   P x 0  . (Μονάδες 10)
Απάντηση:
ΘΕΜΑ 77. 2-22646