91
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
β.
Για
α 4
η εξίσωση γίνεται:
3
2
x
4x
11x 30 0
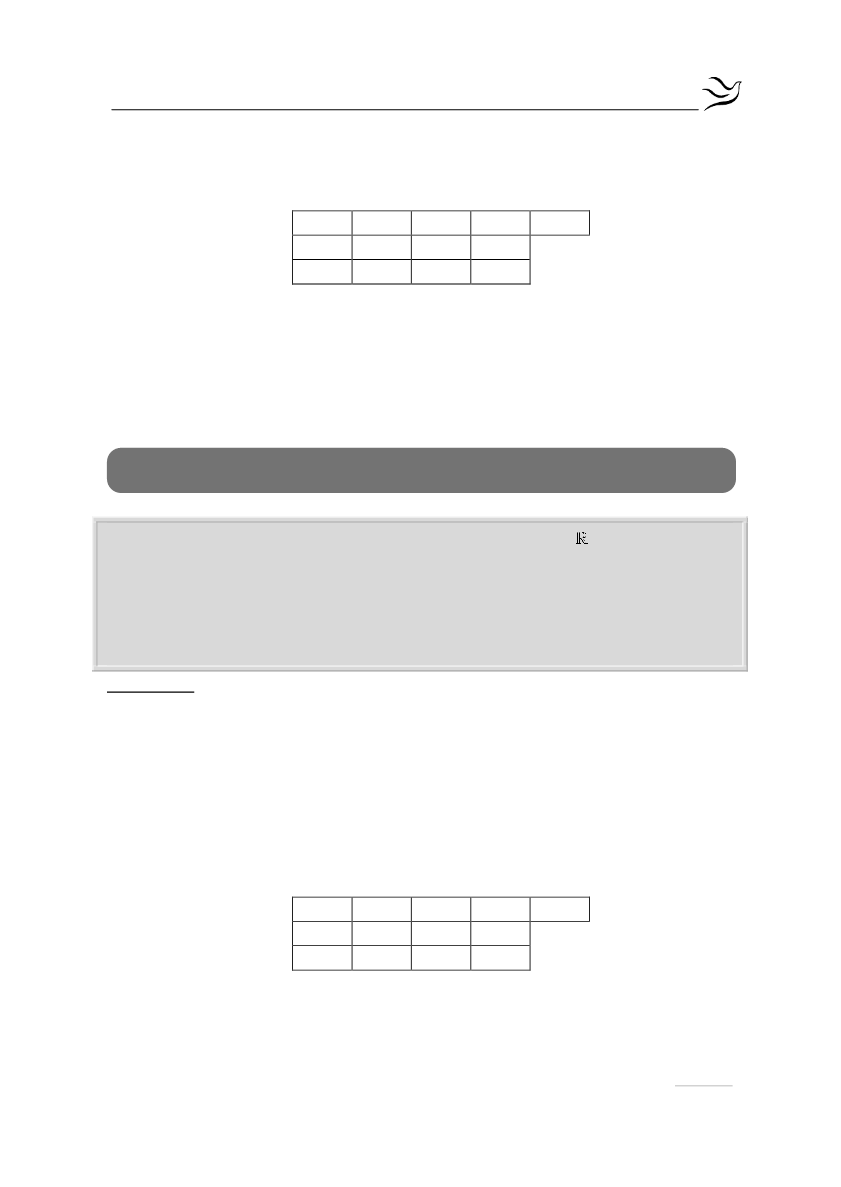
Γνωρίζουμε ότι το 5 είναι ρίζα, οπότε με τη βοήθεια του σχήματος Horner
προκύπτει:
1
-4
-11
30
5
5
5
-30
1
1
-6
0
άρα η εξίσωση γίνεται
2
x 5 x
x 6 0
.
Στη συνέχεια για
2
x x 6 0
προκύπτει
x
3
ή
x 2
, άρα οι λύσεις
της εξίσωσης
P x 0
είναι:
x
3
ή
x 2
ή
x 5
.
Δίνεται το πολυώνυμο
3
2
P x x
αx 11x 30
με
α
, για το οποίο
γνωρίζουμε ότι η τιμή του για
x 1
είναι 16.
α.
Να υπολογίσετε την τιμή του α. (Μονάδες 12)
β.
Αν
α 4
και το 2 είναι ρίζα της εξίσωσης
P x
0
να προσδιορίσετε τις
άλλες ρίζες της εξίσωσης
P x
0
. (Μονάδες 13)
Απάντηση:
α.
Γνωρίζουμε ότι
P 1
16
συνεπώς:
3
2
1
α 1
11 1 30 16
α 20 16
α
4
.
β.
Για
α 4
η εξίσωση γίνεται:
3
2
x
4x
11x 30 0
Γνωρίζουμε ότι το 2 είναι ρίζα, οπότε με τη βοήθεια του σχήματος Horner
προκύπτει:
1
-4
-11
30
2
2
-4
-30
1
-2
-15
0
άρα η εξίσωση γίνεται
2
x 2 x
2x 15 0
.
Στη συνέχεια για
2
x
2x 15 0
προκύπτει ότι οι άλλες ρίζες της
εξίσωσης
P x
0
είναι:
x
3
ή
x 5
.
ΘΕΜΑ 73.
2-22642









