Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

94 / 146

93
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
α. Εφόσον το πολυώνυμο έχει παράγοντα το x 1 , το 1 είναι ρίζα του.
  2 3
P 1 0 λ 1 4λ 1 3 0        
2
λ 4λ 3 0    
λ 1 ή λ 3
β. Για λ 3 το πολυώνυμο γίνεται:
  3 P x 9x 12x 3   
Έχουμε:
3 3
9x 12x 3 0 3x 4x 1 0       
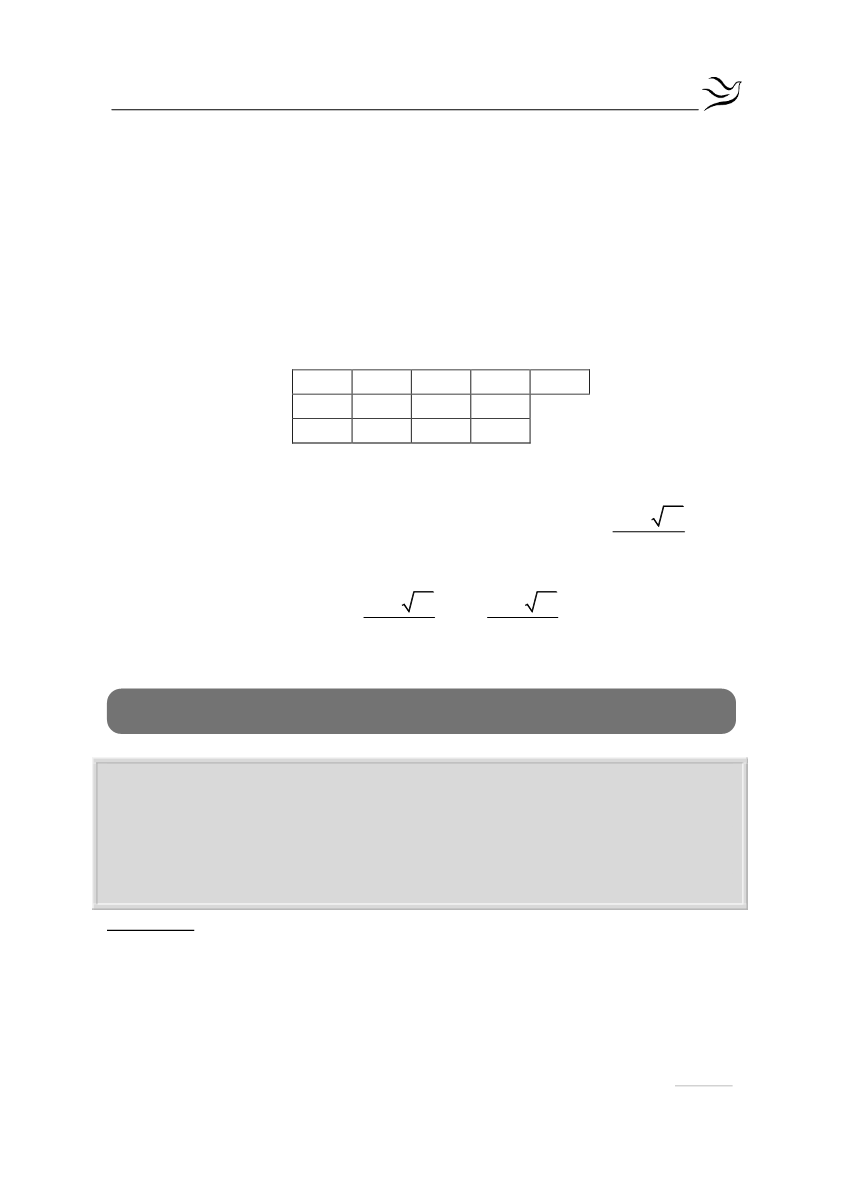
παρατηρούμε ότι το x 1 είναι ρίζα, άρα από το σχήμα Horner έχουμε:
3 0 -4 1 1
3 3 -1
3 3 -1 0
άρα η εξίσωση γίνεται:
   2 x 1 3x 3x 1 0   
και για   2 2
3x 3x 1 0 Δ 3 4 3 1 21           άρα 1,2
3 21
x
6
 
 .
Συνεπώς οι ρίζες του   P x είναι:
x 1 ή
3 21
x
6
 
 ή
3 21
x
6
 
 .
Αν η γραφική παράσταση της συνάρτησης   4 3 2 f x 2x x αx 5x 6    
διέρχεται από το σημείο   M 2,0 ,
α. να αποδείξετε ότι α 14   (Μονάδες 12)
β. να βρείτε τα σημεία τομής της γραφικής παράστασης της συνάρτησης f
με τους άξονες x΄x και y΄y. (Μονάδες 13)
Απάντηση:
α. Το σημείο   M 2,0 ανήκει στη γραφική παράσταση της f συνεπώς
ισχύει ότι:   f 2 0  
          4 3 2
f 2 2 2 2 α 2 5 2 6           
2 32 8 4α 10 6 0       4α 56 α 14     
ΘΕΜΑ 76. 2-22645