Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

120 / 146

119
Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Παρατηρούμε ότι το x 1 είναι μία λύση της εξίσωσης, άρα από το
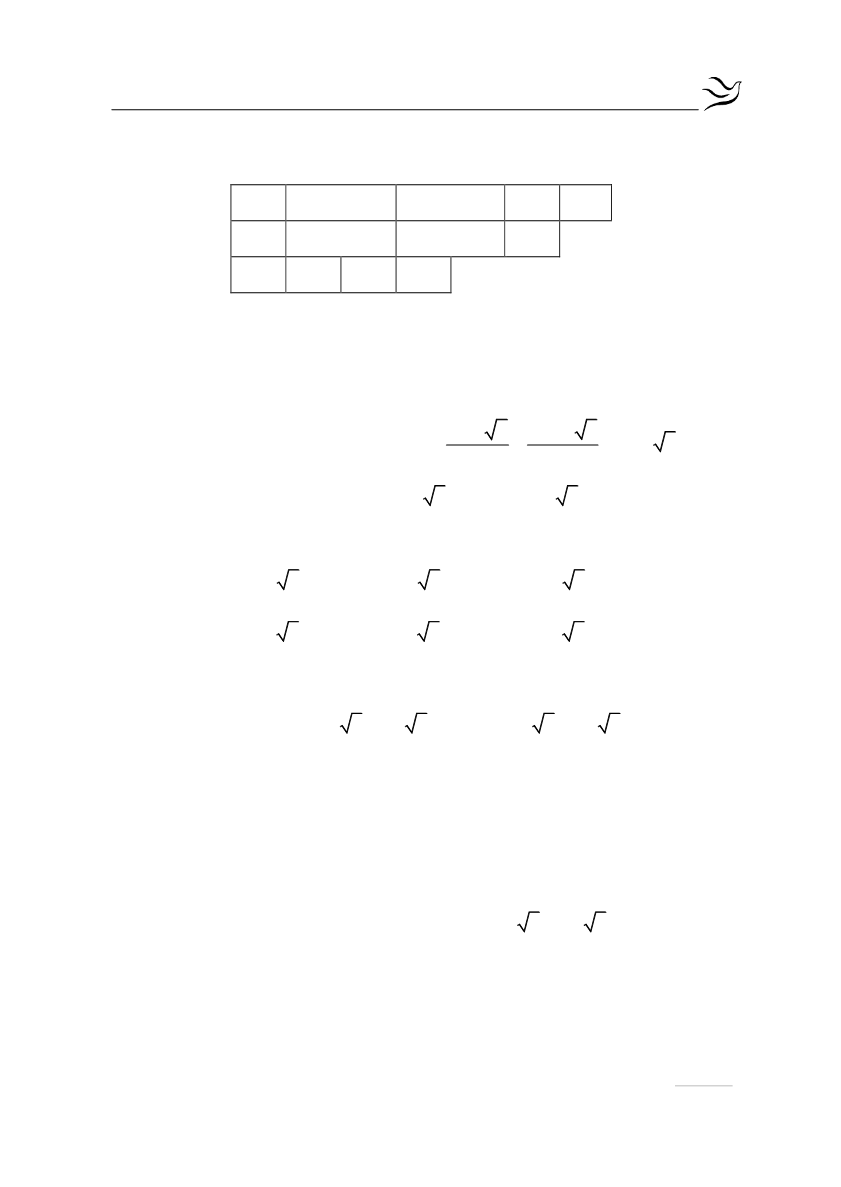
σχήμα Horner θα έχουμε:
1 1 -3 1 1
1 2 -1
1 2 -1 0
άρα η εξίσωση τώρα γίνεται:
   2 x 1 x 2x 1 0   
και για 2
x 2x 1 0   έχουμε:
  2
2,3
2 8 2 2 2
Δ 2 4 1 1 4 4 8 x 1 2
2 2
   
             
Άρα 1 x 1 , 2 x 1 2    και 3 x 1 2    .
 για x 1 y 3 1 1 y 2         
 για  
x 1 2 y 3 1 2 1 y 4 3 2             και
 για  
x 1 2 y 3 1 2 1 y 4 3 2            
άρα τα σημεία τομής της f C και της ευθείας θα είναι τα:
  B 1, 2 ,  
Γ 1 2,4 3 2   και  
Δ 1 2,4 3 2    .
γ. Η ανίσωση 3 2
x x 3x 1      έχει ως λύσεις τα διαστήματα στα οποία η
γραφική παράσταση της f βρίσκεται κάτω από την ευθεία y 3x 1    .
Από τις γραφικές τους παραστάσεις βλέπουμε ότι αυτό συμβαίνει από το
σημείο Δ μέχρι το Γ και από το Β μέχρι το  .
Δηλαδή, η λύση της ανίσωσης είναι:     x 1 2, 1 2 1,        .