Αλγεβρα Β' Λυκείου (Τράπεζα Θεμάτων)

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Β’ Γενικού Λυκείου

118

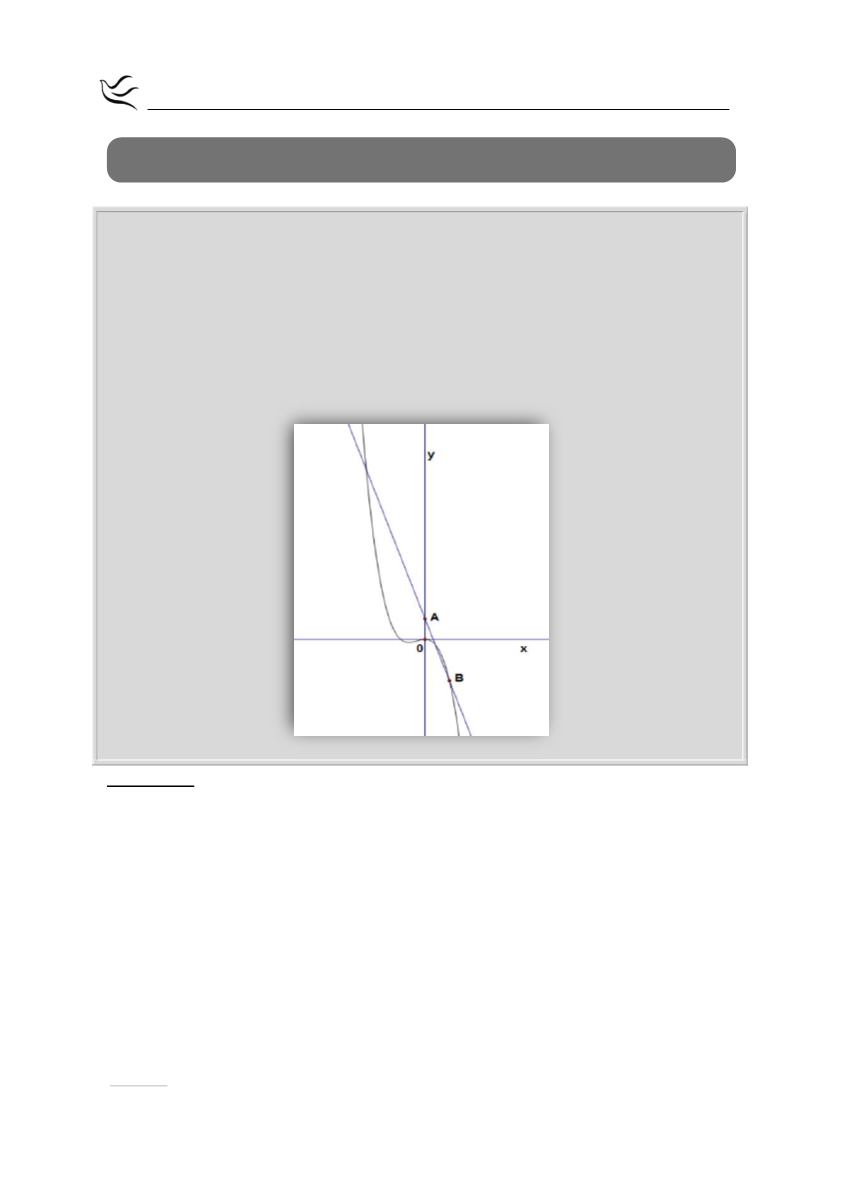
Στο σχήμα φαίνονται η γραφική παράσταση της συνάρτησης

 

f x

  

και

η ευθεία που διέρχεται από τα σημεία





A 0,1

και





B 1, 2



α.

Να βρείτε την εξίσωση της ευθείας. (Μονάδες 7)

Αν η ευθεία έχει εξίσωση

y 3x 1

  

, να βρείτε τις συντεταγμένες των

κοινών σημείων της ευθείας με την γραφική παράσταση της

(Μονάδες 9)

β.

Να λύσετε την ανίσωση

3 2

x 3x 1

 

  

. (Μονάδες 9)

Απάντηση:

α.

Εφόσον

A B

x x



ξέρουμε ότι η εξίσωση της ευθείας θα έχει τη μορφή

y αx β

 

Αφού η ευθεία διέρχεται από το





A 0,1

έχουμε ότι:

1 α 0 β β 1



   

Και από το





B 1, 2



παίρνουμε ότι:

2 α 1 β 2 α 1

 

       

Άρα η εξίσωση της ευθείας είναι:

3x 1

  

β.

Για να βρούμε τις συντεταγμένες των κοινών σημείων της ευθείας με την

γραφική παράσταση της

αρκεί να λύσουμε την εξίσωση:

 

3 2

f x 3x 1 x

3x 1

        

3 2

x x

3x 1 0





 

ΘΕΜΑ 97.

4-22777