Αλγεβρα A' Λυκείου (Τράπεζα Θεμάτων)

187 / 240

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Άλγεβρας Α’ Γενικού Λυκείου
186
 5 1 5 1
ω ω 3 ή ω=
2 1 2
   
   

2
Έτσι,
     
x ω
2 ω 5ω 6 ω 3 ω 2 x 3 x 2

       
Άρα
 
   2 x 3 x 2 x 5 x 6
f x x 2
x 3 x 3
   
   
 
και x A
γ. Έχουμε,
         
ερωτ.2 2 2 2
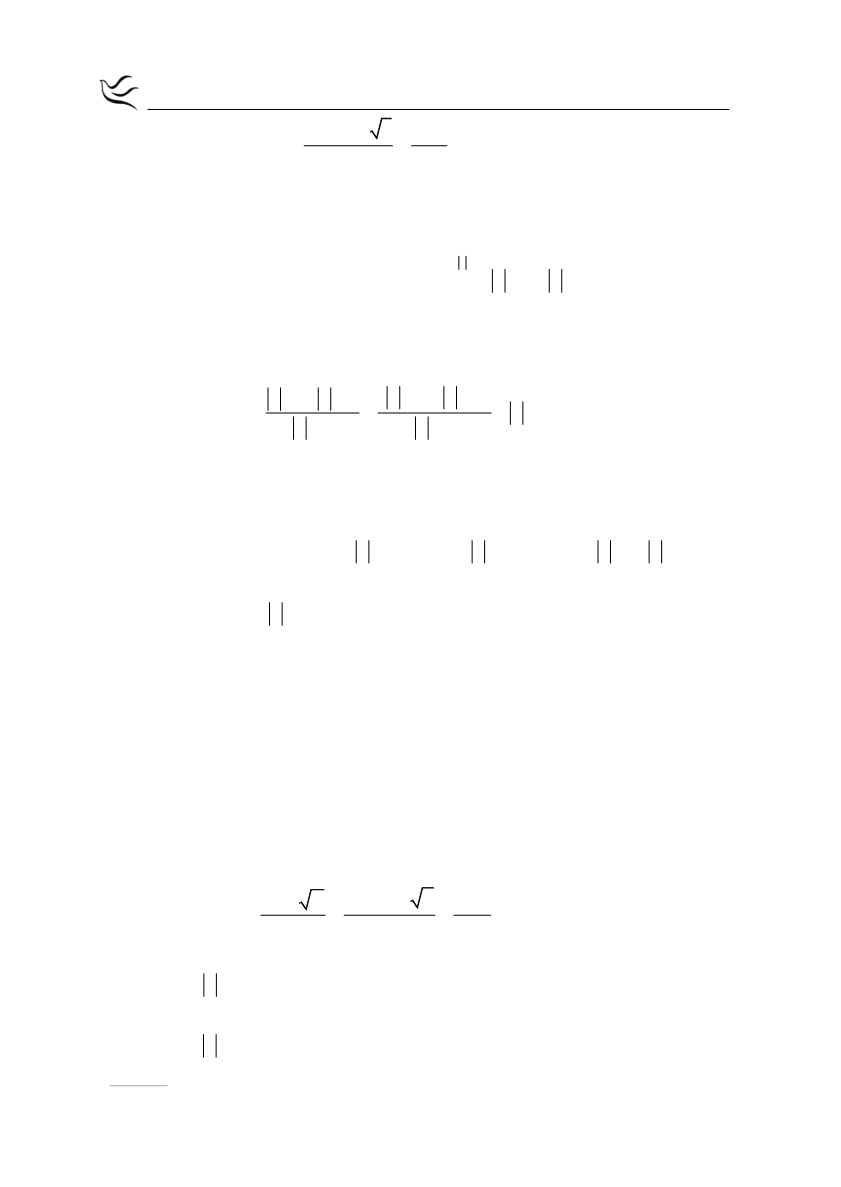
x 2 x f x 2 4f x 5 0 2 4 5 0 x 4 x 3 0 2               ,
x A και θεωρούμε x ω 0  , οπότε η τελευταία εξίσωση ισοδύναμα,
2 ω 4ω 3 0   
με
 2
2 Δ β 4αγ 4 4 1 3 4 0         
και έχει ρίζες
 4 4 β Δ 4 2
ω ω 3 ή ω=1
2α 2 1 2
     
    

Αν ω 3 x 3 Α    και απορρίπτεται.
Αν ω 1 x 1 x 1       δεκτές ρίζες.