Μαθηματικά Γ' Λυκείου (Γενικής Παιδείας)

83 / 234

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά και Στοιχεία Στατιστικής
82
2 2 11 2 1 2
x x 0 15x 11x 2 0 x ή x
15 15 3 5
- + = Û - + = Û = = .
· ( ) ( ) 2 2 11 2 11 2
f ' x 0 f x x x 0 x x 0
15 15 15 15
æ ö
> Û × - + > Û - + >
ç ÷
è ø
,αφού ( )
f x 0>
άρα θα έχουμε: 2 2 11 2
x x 0 15x 11x 2 0
15 15
- + > Û - + > , η οποία
αληθεύει, όταν
1 2
x , ,
3 5
æ ö æ ö
Î -¥ È +¥
ç ÷ ç ÷
è ø è ø
.
· Ομοίως, ( ) 1 2
f ' x 0 x ,
3 5
æ ö
< Û Î ç ÷
è ø
.
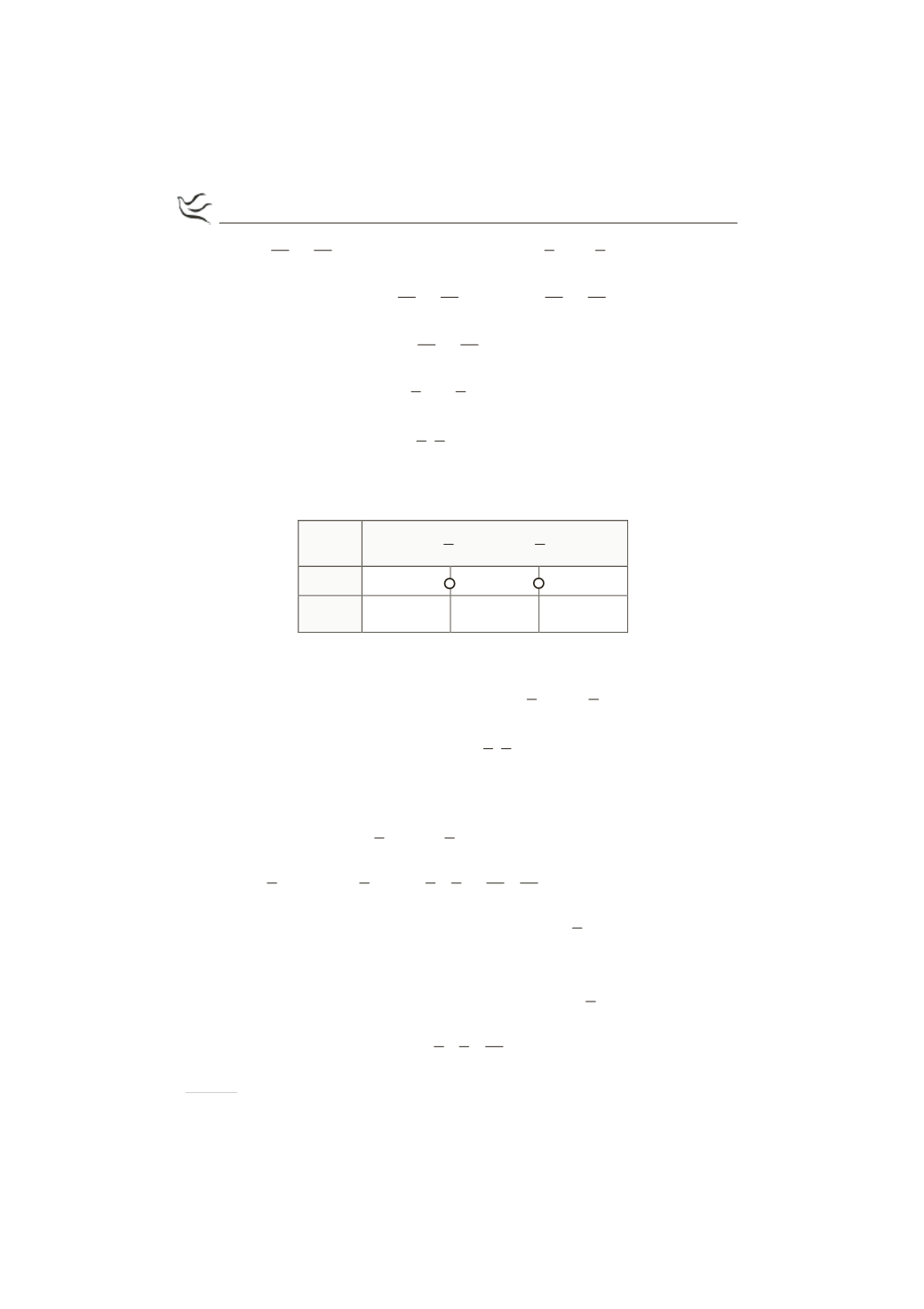
Ακολουθεί ο πίνακας μεταβολών της συνάρτησης f:
x
1 2
3 5
-¥ +¥
( )
f ' x + - +
f 1 > 1
Άρα, η συνάρτηση είναι:
· Γνησίως αύξουσα στα διαστήματα:
1
,
3
æ ù -¥ç
ú
è û
και
2
,
5
é ö
+¥ ÷
êë ø
· Γνησίως φθίνουσα στο διάστημα
1 2
,
3 5
é ù
ê ú ë û .
Δ2. Στον παραπάνω πίνακα, παρατηρούμε ότι η f παρουσιάζει τοπικά
ακρότατα στα σημεία
1
x
3
= και
2
x
5
= . Εφόσον A BÍ , θα είναι ( ) ( )
P A P B£ ,
άρα ( ) 1
P A
3
= και ( ) 2
P B
5
= , γιατί
1 2 5 6
3 5 15 15
< Û < . Ισχύουν:
· A BÍ , άρα A B AÇ = , οπότε ( ) ( ) 1
P A B P A
3
Ç = =
· A BÍ , άρα A B- =Æ , συνεπώς ( ) ( )
P A B P 0- = Æ =
· A BÍ , επομένως A B BÈ = και ( ) ( ) 2
P A B P B
5
È = =
· ( ) ( ) ( ) 2 1 1
P B A P B P B A
5 3 15
- = - Ç = - = .
T.M. T.E.