39
Μαθηματικά και Στοιχεία Στατιστικής – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
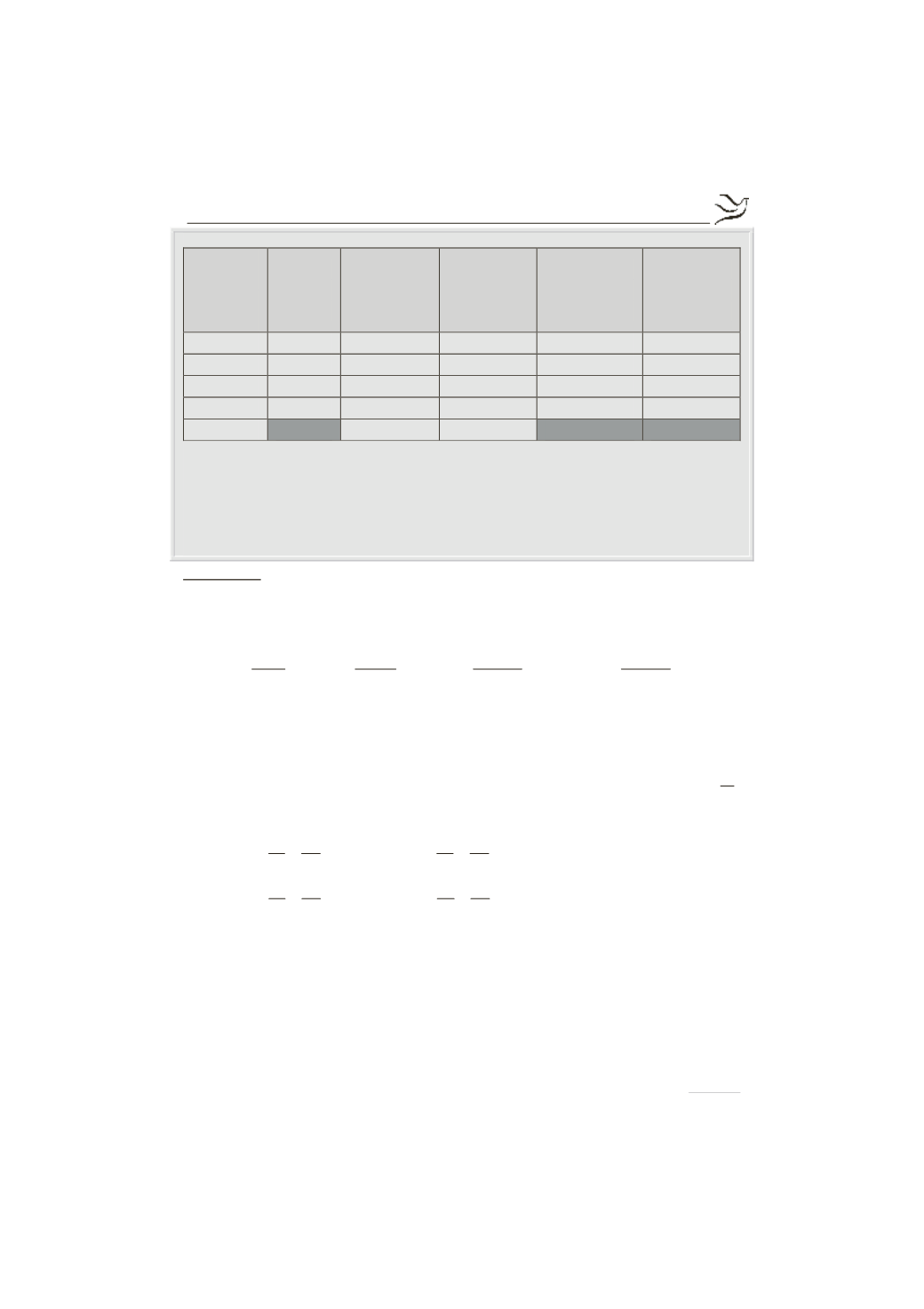
Κλάσεις
βαθ/γίας
[ )
Κέντρο
κλάσης
x
i
Συχνότητα
ν
i
Σχετική
Συχνότητα
f
i
Αθροιστική
Συχνότητα
Ν
i
Αθρ. Σχετ.
Συχνότητα
F
i
[4, 8)
[8,12)
[12,16)
[16,20)
Σύνολο
(
Μονάδες 11
)
β.
Να βρείτε τη μέση τιμή των βαθμών.
(
Μονάδες 8
)
γ.
Πόσοι μαθητές έχουν βαθμό μέχρι και 10;
(
Μονάδες 6
)
Απάντηση:
α.
Έχουμε για τη συμπλήρωση του πίνακα:
·
Το κέντρο κάθε κλάσης ισούται με το ημιάθροισμα των άκρων του
διαστήματος, έτσι:
1
4 8
x
6
2
+
= =
,
2
8 12
x
10
2
+
=
=
,
3
12 16
x
14
2
+
=
=
και
4
16 20
x
18
2
+
=
=
·
Σύμφωνα με το δοθέν ιστόγραμμα συχνοτήτων είναι:
1
ν 5
=
,
2
ν 10
=
,
3
ν 25
=
και
4
ν 10
=
·
1 2 3 4
ν ν ν ν ν 50
= + + + =
.
·
Θα υπολογίσουμε τις σχετικές συχνότητες
i
f
από τον τύπο
i
i
ν
f
ν
=
,
i 1,2,3,4
=
:
1
1
ν
5
f
0,1
ν 50
= = =
,
2
2
ν
10
f
0,2
ν 50
= = =
,
3
3
ν
25
f
0,5
ν 50
= = =
,
4
4
ν
10
f
0,2
ν 50
= = =
.
·
Έχουμε για τις αθροιστικές συχνότητες
:
1 1
Ν ν 5
= =
, ενώ από τον τύπο:
i
i 1 i
Ν Ν ν
-
= +
για
i 2,3,4
=
, προκύπτει:
2
N 15
=
,
3
N 40
=
και
4
N 50
=
.
·
Έχουμε
για τις αθροιστικές σχετικές συχνότητες:
1 1
F f 0,1
= =
, ενώ από τον τύπο:
i
i 1 i
F F f
-
= +
για
i 2,3,4
=
, προκύπτει:
2
F 0,3
=
,
3
F 0,8
=
και
4
F 1
=
.









