Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
60
Πρόταση
Αν μια
συνάρτηση
f
παρουσιάζει κρίσιμο σημείο
σε
ένα σημείο
0
x
του πεδίου ορισμού της
τότε παρουσιά-
ζει υποχρεωτικά και τοπικό ακρότατο στο
0
x
.
Απάντηση
Λάθος
Αντιπαράδειγμα
Έστω η
( )
(
)
3
2
x , x 1
f x
x 2 , x 1
ì
<
ï
= í
- ³
ïî
,
Η f
είναι συνεχής στο
R
και
παραγωγίσιμη στο
R
εκτός
από το 1 με
( )
(
)
2
3x , x 1
f x
2 x 2 , x 1
ì
<
ï ¢
= í
- >
ïî
Οι ρίζες της
( )
f x 0
¢
=
είναι το
0 και το 2.
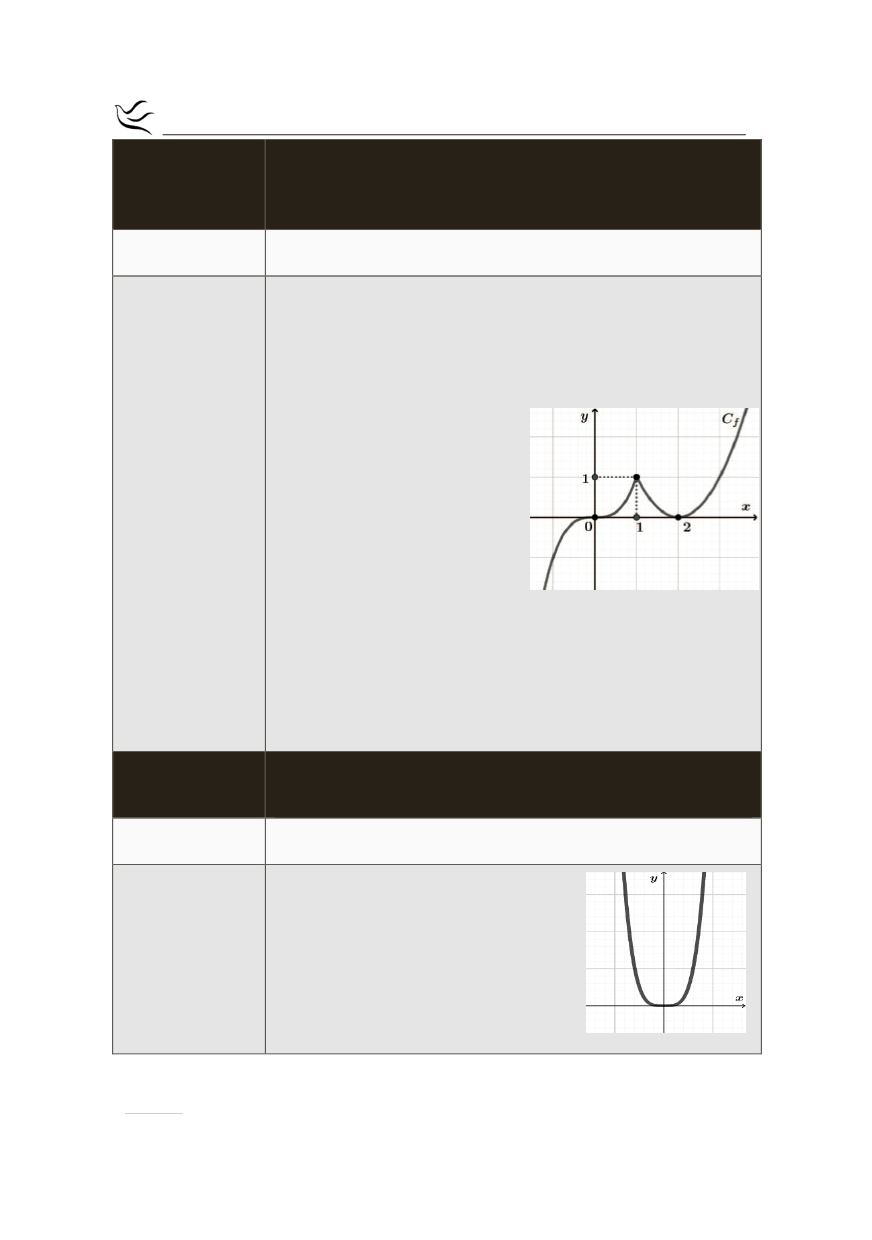
Επειδή η f΄ μηδενίζεται στα
σημεία 0 και 2, ενώ δεν υπάρ-
χει στο
1, τα
κρίσιμα σημεία
της f είναι οι αριθμοί
0,
1 και
2.
Όμως όπως φαίνεται στο σχή-
μα το
σημείο 0 δεν είναι θέση
τοπικού ακροτάτου
.
Πρόταση
Για κάθε κυρτή και 2 φορές παραγωγίσιμη
συνάρτη-
ση σε ένα διάστημα Δ ισχύει
( )
f x 0
¢¢
>
για κάθε
x
Δ
Î
.
Απάντηση
Λάθος
Αντιπαράδειγμα
Η
συνάρτηση
( )
4
f x x
=
,
αν και είναι κυρτή
στο
!
, εντούτοις έχει δεύτε-
ρη παράγωγο
( )
2
f x 3x
¢
=
η οποία δεν είναι θετική
σε όλο το
!
, αφού
( )
f 0 0
¢
=
.









