59
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Πρόταση
Αν για μια συνάρτηση
f
ισχύει
( )
f x 0
¢
=
για κάθε
x
Α
Î
(Α: σύνολο) τότε η f
είναι υποχρεωτικά σταθερή.
Απάντηση
Λάθος
Αντιπαράδειγμα
Έστω η συνάρτηση
( )
1 , x 0
f x
1 , x 0
-
<
ì
= í
>
î
.
Παρατηρούμε ότι, αν και
( )
f x 0
¢
=
για κάθε
x ( ,0) (0,
)
Î -¥ È +¥
, εντούτοις η
f
δεν είναι σταθερή
στο
( ,0) (0, )
-¥ È +¥
.
Πρόταση
Για κάθε γνησίως αύξουσα
και παραγωγίσιμη
συνάρ-
τηση σε ένα διάστημα Δ ισχύει
( )
f x 0
¢
>
για κάθε
x
Δ
Î
.
Απάντηση
Λάθος
Αντιπαράδειγμα
Η
συνάρτηση
( )
3
f x x
=
, αν και εί-
ναι γνησίως αύξουσα στο
!
, ε-
ντούτοις
έχει
παράγωγο
( )
2
f x 3x
=
η οποία δεν είναι θετι-
κή σε όλο το
!
, αφού
( )
f 0 0
¢
=
.
Πρόταση
Αν μια
συνάρτηση
f
παρουσιάζει τοπικό ακρότατο
σε
ένα σημείο
0
x
του πεδίου ορισμού της
τότε παρουσιά-
ζει υποχρεωτικά και ολικό ακρότατο στο
0
x
.
Απάντηση
Λάθος
Αντιπαράδειγμα
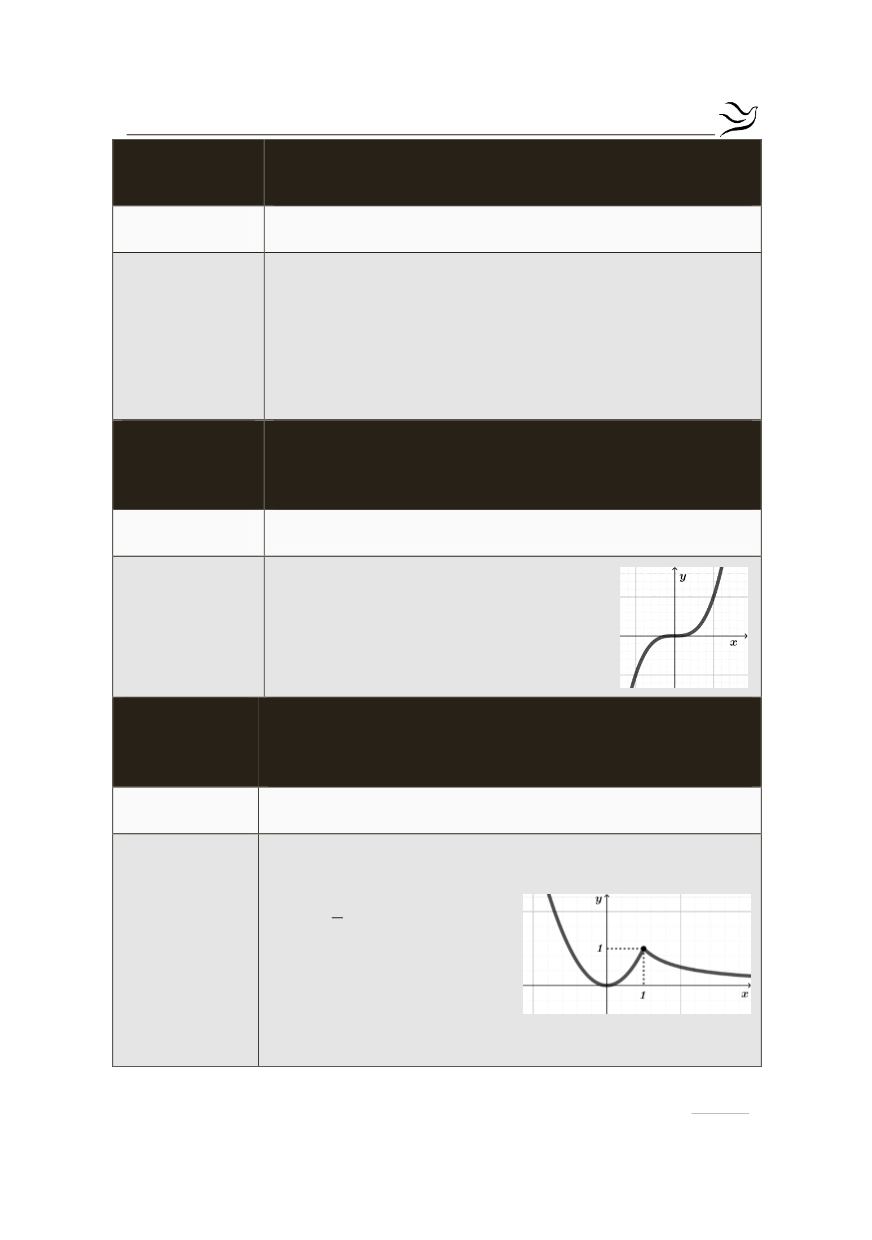
Η
συνάρτηση
( )
2
x , x 1
f x 1
, x 1
x
ì £
ï
= í
> ïî
, αν και πα-
ρουσιάζει τοπικό μέγιστο
στο
0
x 1
=
, εντούτοις δεν
παρουσιάζει (ολικό) μέγι-
στο.









