169
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
β.
Η
f
είναι δύο φορές παραγωγίσιμη στο
(
)
0,
+¥
με
( ) (
)
1
f x 2x lnx x 2lnx 2x 1
x
¢
¢¢
= ×
+ = + × + =
2lnx 2 1 2lnx 3
+ + = +
.
( )
¢¢
= Û
f x 0
-
+ = Û = - Û =
3
2
3
2lnx 3 0 lnx
x e
2
( )
3
3
lnx
2
2
3
f x 0 2lnx 3 0 lnx
lnx lne x e
2
-
-
¢¢
> Û + > Û > - Û > Û >
1
( )
3
3
lnx
2
2
3
f x 0 2lnx 3 0 lnx
lnx lne x e
2
-
-
¢¢
< Û + < Û < - Û < Û <
1
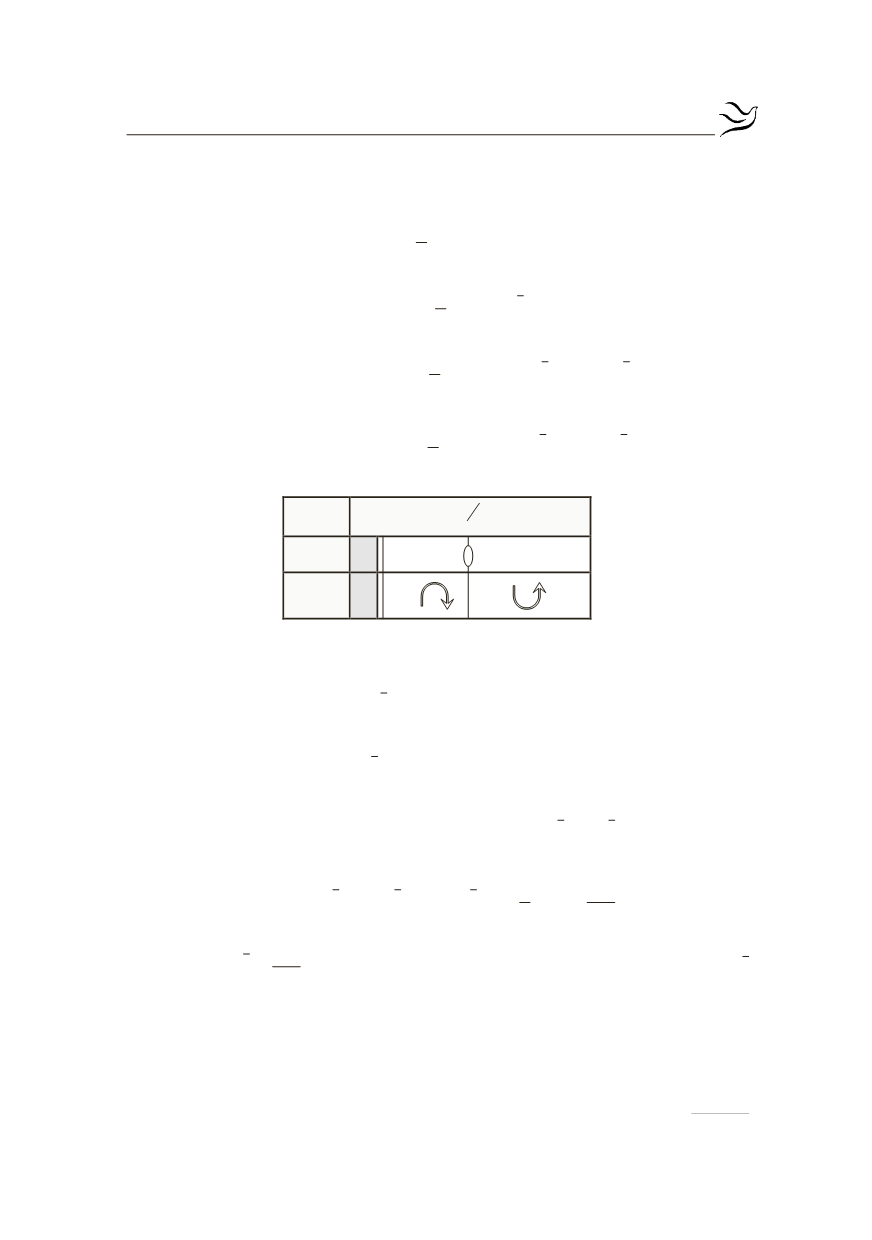
Από τον παραπάνω πίνακα προκύπτει ότι:
·
Η
f
είναι κοίλη στο
3
2
0,e
-
æ
ù
ç
ú
è
û
·
Η
f
είναι κυρτή στο
-
é
ö
+¥ ÷
ê
ë
ø
3
2
e ,
Επιπλέον η
f
έχει σημείο καμπής το σημείο
3
3
2
2
M e ,f e
-
-
æ
ö
æ ö
ç
÷
ç ÷
ç
÷
è ø
è
ø
με
2
3
3
3
3
2
2
2
3
3
3
f e
e ln e
e
2
2e
-
-
-
-
æ ö æ ö æ ö
=
×
= - = -
ç ÷ ç ÷ ç ÷
è ø è ø è ø
Άρα
-
æ
ö
- ç
÷
è
ø
3
2
3
3
M e ,
2e
,
αφού η
¢¢
f
αλλάζει πρόσημο εκατέρωθεν του
-
=
3
2
0
x e
και η
f
παραγωγίσιμη στο σημείο αυτό άρα ορίζεται εξίσωση εφαπτομένης
.
x
0
3
2
e
-
+¥
( )
f x
¢¢
-
+
f
l o









