Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
168
α.
Πρέπει
x 0
>
. Άρα
,
(
)
= +¥
f
D 0,
και
f
συνεχής ως γινόμενο συνεχών συναρ-
τήσεων (
lnx
λογαριθμική και
2
x
πολυωνυμική)
H
f
είναι παραγωγίσιμη στο διάστημα
(
)
+¥
0,
με
( )
(
) ( )
( )
2
2
2
f x x lnx x lnx x lnx
¢
¢
¢
¢
= ×
= ×
+
=
(
)
2
1
2x lnx x
2x lnx x x 2lnx 1
x
= ×
+ × = ×
+ = ×
+
( )
¢
= Û
f x 0
(
)
1
lnx
x 0
2
1
x 2lnx 1 0 2lnx 1 0 lnx
x e
2
>
-
×
+ = Û + = Û = - Û =
1
( )
f x 0
¢
> Û
(
)
1
lnx
x 0
2
1
x 2lnx 1 0 2lnx 1 0 lnx
x e
2
>
-
×
+ > Û + > Û > - Û >
1
( )
f x 0
¢
< Û
(
)
1
lnx
x 0
2
1
x 2lnx 1 0 2lnx 1 0 lnx
0 x e
2
>
-
×
+ < Û + < Û < - Û < <
1
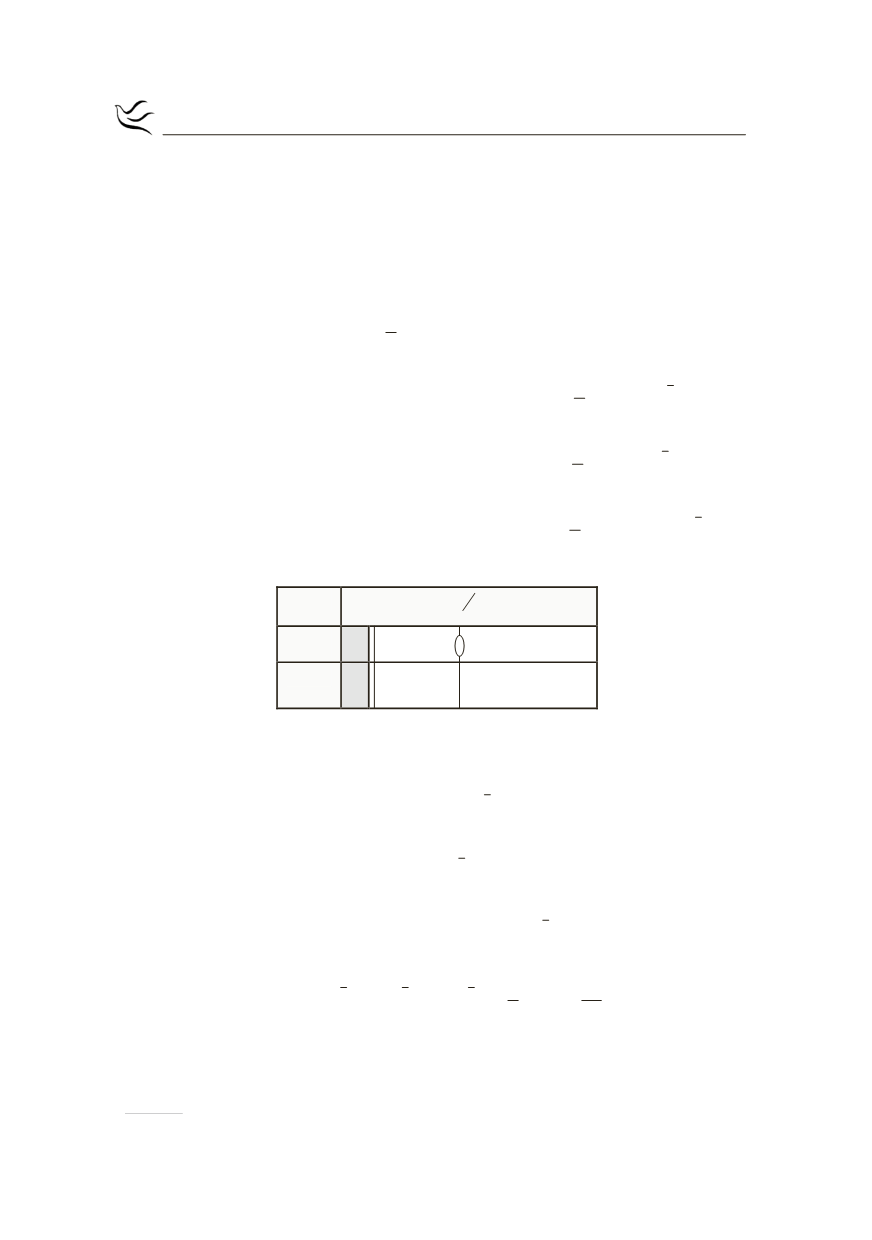
Από τον παραπάνω πίνακα μεταβολών έχουμε ότι
·
Η
f
είναι γνησίως φθίνουσα στο
1
2
0,e
-
æ
ù
ç
ú
è
û
·
Η
f
είναι γνησίως αύξουσα στο
1
2
e ,
-
é
ö
+¥ ÷
ê
ë
ø
Επιπλέον
παρουσιάζει ολικό ελάχιστο για
-
=
1
2
x e
το
2
1
1
1
1
2
2
2
1
1
f e
e lne
e
2
2e
-
-
-
-
æ ö æ ö
=
×
= - ×
= -
ç ÷ ç ÷
è ø è ø
.
x
0
1
2
e
-
+¥
( )
¢
f x
-
+
f
> 1









