Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Σε ορθογώνιο τρίγωνο ΑΒΓ (
0
Α 90
=
), η διχοτόμος της γωνίας
Γ
τέμνει την
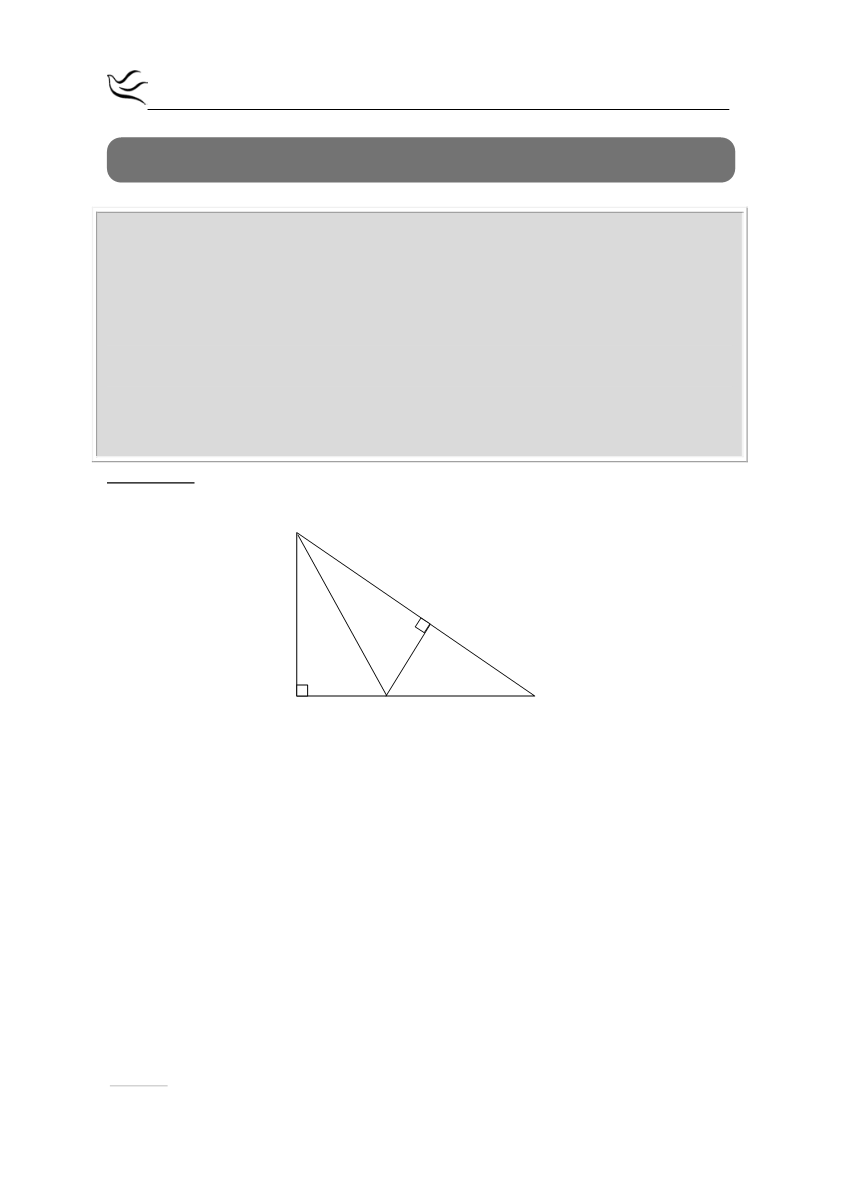
πλευρά ΑΒ στο σημείο Δ. Από το Δ φέρουμε προς την πλευρά ΒΓ την κάθετο ΔΕ,
η οποία τέμνει τη ΒΓ στο σημείο Ε . Να αποδείξετε ότι:
α) ΑΔ=ΔΕ
(Μονάδες 13)
β) ΑΔ<ΔΒ.
(Μονάδες 12)
Απάντηση:
α) Επειδή το σημείο Δ ανήκει στη διχοτόμο της γωνίας
Γ
, θα ισαπέχει από τις
πλευρές της ΓΑ και ΓΒ. Επομένως, θα είναι
ΑΔ
=
ΔΕ (1).
β) Στο ορθογώνιο τρίγωνο ΔΕΒ η πλευρά ΔΒ είναι η υποτείνουσα. Επομένως, θα
είναι
ΔΕ < ΔΒ (2).
Από τις σχέσεις (1) και (2) συμπεραίνουμε ότι
ΑΔ < ΔΒ.
Α
Γ
Δ
Ε
Β
ΘΕΜΑ 2837
8









